Math 101 STUDY GUIDE
| Sect/Pg |
Problems |
Problem Type |
| 1.1/ 10 |
55,59,67 |
Integer Order of Operations |
| 1.2/ 19 |
41,49,61,69 |
More Order of Operations |
| WS#1 |
1,11,36,46 |
More Order of Operations |
| 1.3/ 28 |
27,29,41,45 |
Order of Operations with Exponents |
| 1.4/ 36 |
15,21,41,65,69,75 |
Simple Algebraic Expressions, Evaluating with
Substitution, English Phrases Translated
into Algebraic Expressions |
| WS#2 |
6,78 |
Order of Operations and Parentheses |
| 2.1A/ 50 |
11,27,39,49 |
Solve Linear (1st degree) Equations with
Integers |
| WS#4 |
6,8,18,19,26,29,44,5
1 |
Solve Basic Linear Equations (These are
problems of types from 2.1A; 2.2A; 2.3A; & 2.4A,
but basically short .. Good practice.) |
| 2.1B/51 |
51,53,55,57 |
Word Problems: "Number Type" |
| 2.2A/58 |
3,9,29,37 |
Solve 1st Degree Equations with Fractions:
Remember you can multiply both sides of the
equation by the LCD to "remove the fractions" from the equation.
The safest way is to multiply
each term by the LCD. |
| 2.2B/ 59 |
41,45,53 |
Word Problems: "Number Type" with Fractions |
| 2.2C/ 59 |
43,47,55 |
Word Problems: "Geometry" with Fractions |
| 2.3A/ 66 |
1,9,15,23 |
Solve Decimal Equations : Same idea as the
fractional equations... You can multiply each
term by the correct multiple of 10 to "remove the decimal". Be careful
to "add zero's" when
needed in this process. |
| 2.3B/ 67 |
29,35,41,43 |
Word Problems: Percents & Decimals |
| WS#15 |
1,3,4,11,12 |
Word Problems: Percents & Decimals |
| 2.4A&B/ 77 |
1,7,9,19,25 |
Symbolic Linear Equations: Solving for One
Variable "in Terms of" or by Substitution:
Solve for the unknown cited and treat the other unknowns "like they were
constants", adding,
sutracting, multiplying and dividing by them as needed just like you
would if they were
numbers. Warning: You have not "solved for the given unknown if
it is "in the answer"
(Example: x = 3x + c is NOT solved for x.) |
| 2.4C/ 78 |
31,45 |
Symbolic Linear Equations that Require
Factoring to SOLVE : Similar to the above
problems but these have more than one term left with the desired unknown
once all possible
terms have been combined. Have all terms that have the desired unknown
on one side of the
equation and all other terms on the other side of the equation. Then the
desired unknown can
be factored out as a common factor on that side. Divide both sides by
the quantity left in ( ),
and you will have solved for the desired unknown. |
| WS#20 |
2,5,9,44,45 |
Symbolic Linear Equations that Require
Factoring to SOLVE |
| 2.4D/ 78 |
47,48 |
Word Problems: "Geometry" |
| 2.4E/78 |
49, 51 |
Word Problems: Percents & Decimals:
Remember that percents must be changed to
decimals by shifting the decimal place 2 positions to the left. Also,
remember that "percents
never stand alone": A percent OF something indicates to
multiply the decimal equivalent
times that something. |
| 2.4G/78 |
59, 61 |
Word Problems: Mixture |
| WS#16 |
15,18,20 |
Word Problems: Mixture |
| 2.5A/ 85 |
1,7,11,13,17 |
Linear Inequalities: Notation: Se sure you
can use the "new" Number Line notation and
that you can put these into Interval Notation, and vice versa. |
| 2.5B/ 85 |
31,37,45,59,63 |
Linear Inequalities: Solving: Remember to keep
the inequality symbol facing the same
direction as you go, solving the same way you would solve a linear
equation, except: If you
multiply or divide by a negative number , then you must reverse
the direction of the
inequality symbol. Be able to put your answer in any of the 3 forms
(Inequality, Number Line,
or Interval Notation.) |
| 3.1/114 |
Also WS#6) |
Polynomial Sums & Differences |
| 3.2/120 |
5,33,49,51,53,63,65 |
Monomial Products & Quotients: USING EXPONENT
RULES |
| 3.3/127 |
3,9,21,25,37,55,63 |
Multiplying Polynomials (Includes FOIL) |
| WS#10 |
1,9,25,46 (See
also WS#8) |
Multiplying Polynomials (Includes FOIL) |
| WS#7 |
3,12,24,29,30,47 |
A mixture of Multiplying and Adding
Polynomials |
| |
WARNING** |
On the Final: Be sure to pay attention to
directions as to whether you are to JUST
FACTOR, or SOLVE an equation so that you do NOT confuse these problems
from 3.4 -
3.7! |
| 3.4A&B/135 |
25,39,45,51,55 |
FACTORING: by Common Factors & by Grouping |
| 3.4C/136 |
65,71,75 |
SOLVING EQUATIONS BY FACTORING |
| 3.5A&B/142 |
5,15,25,39 |
FACTORING: Difference of Squares (Difference
of Cubes may be used for Bonus |
| 3.5C/ 143 |
57,61,63,67 |
SOLVING EQUATIONS BY FACTORING |
| 3.6A/151 |
1,17,25,39,47,53;
See also WS#11 |
FACTORING: FOIL Type |
| 3.6B/151 |
57,61,67,73,77,85,9
3 |
FACTORING: All Methods: Remember to
always: 1. Check for Greatest common factor
first, once that is done... 2. Count the number of terms to
help identify the factoring pattern:
Two terms: Difference of squares or difference of cubes (the latter will
NOT be on the Final);
Three terms: Foil factor (or trinomial factoring.); Four terms:
Possibly by grouping. Always
factor COMPLETELY! See warning** above. |
| WS#12 |
1,5,24,40,47 |
FACTORING: All Methods |
| 3.7A/157 |
1,17,27,41,53 |
SOLVING EQUATIONS BY FACTORING: These are
equations that have a 2nd degree term
or higher. The idea is to: 1. get your equation set = 0 with
terms combined, etc., 2. Then
completely factor that expression. Once it is in factored form, 3.
set each factor = 0, since
the only way a product can be 0 is for one or more of the factors to be
0. For most of these
problems, these factors will either be numbers that can not be 0, or
will be simple linear
expressions that can be easily solved. See warning** above. |
| 3.7B/157 |
55,57,59,61 |
Word Problems: Not assigned.. Possible Bonus
Problems..Equation found will be solved
by factoring methods |
| 4.1/171 |
13,17,21,29,45 |
Simplifying Rational Expressions (Algebraic
Fractions): Remember you can only "cancel"
factors (things that are multiplied both top & bottom. Hint: This
requires that there can be only
ONE term top and bottom before cancellation can be considered.
Remember proper
exponent rules, and where there are polynomials, get these
into completely factored form
in order to simplify. |
| 4.2/177 |
15,21,25,27,39 |
Simplifying Rational Expressions: Multiply &
Divide: Same idea as above. Remember to
invert to multiply in the case of division before doing any
cancellation. Once things are in
factored form and multiplied, you can "cancel" same factors top to
bottom whether they are in
the same fraction or in a different one, as long as one is on top and
one is on bottom. |
| 4.3/185 |
9,15,23,31,41,51,
63; See also
WS#21 |
Simplifying Rational Expressions: Add &
Subtract : This is just like adding and subtracting
number fractions, you must get a common denominator and it is
very important to get the
Least Common Denominator. Remember in "creating" the LCD, you are
essentially
multiplying each fraction by an equivalent of "one" so that the
value of your expression
does not change. Warning: Do not confuse this with solving
equations that contain
fractions. In Section 2.3, you could multiply by the LCD and remove the
fractions, but now
you are Simplifying, and if you multiply by the LCD, you are changing
the value of your
expression.. BAD! |
| 5.1A/232 |
7,25,35,37,39 |
Integers as Exponents with Numbers:
Exponent rules are the same even though we are
now considering negative integer exponents also. The negative
exponent just means to take
the inverse of whatever is raised to that exponent. If everything
is multiplied and/ or divided,
this essentially means that you can "move" a factor with its exponent
"down" or "up" in a
fraction by changing the sign of its exponent. Refer to class notes for
rules and examples.
Warning: A negative exponent does NOT make the number
negative. (Example 3 "to the -1
power" does NOT equal -3... It is equal to 1/3. Be sure to "evaluate"
all numbers raised to
exponents... That is, get a number equivalent. (Example, don't
leave 5 raised to the 3rd
power... This should be evaluated as 125.) |
| 5.1B/232 |
43,53,57,59,71 |
Integers as Exponents with Algebraic
Expressions: Same principles as above, except that
you will not be able to evaluate a variable raised to a power. NEVER
leave a negative
exponent in an answer. |
| 5.1C/232 |
75,81,83 |
Integers as Exponents with Algebraic
Expressions with 2 Terms: When more than one
term is involved, then you are not in factored form. First, change
each factor to the correct
position with a positive exponent instead of a negative one. Now, it
will probably "look
like" an addition of fractions problem like those in 4.3. Proceed as
with those problems. |
| WS#18 |
3,4,5,6,7,11,14,16,1
9,23,24,28,36,39,43 |
Basic Exponent Problems |
| 5.2A/243 |
1,3,5,7,15 |
Basic Radicals with Numbers: These "come
out of the radical exactly." |
| WS#3 |
2,6,8,11,19,20,39,53 |
Basic Radicals with Numbers |
| 5.2B/243 |
23,31,35,41 |
Simplifying Radicals with Numbers: Here,
"split the number into factors" so that one is a
perfect square (hopefully the largest one possible.) and the other is
not. Take the square root
of the perfect square and multiply it on the "outside" and leave the
other number "inside." If
you did not find the largest perfect square the first time, you will
have to repeat this process. |
| WS#13 |
2,8,32,41,43 |
Simplifying Radicals with Numbers |
| 5.2C/244 |
45,51,61,69,73 |
Simplifying Radicals: Rationalizing
Denominators with Square & Cube Roots with
Numbers Only. To "rationalize the denominator" means to
"remove the radical(s) from the
denominator". This must be done in such a way that the "value of the
expression" is not
changed. Same concept of not changing value as we faced with
fraction expressions, so
whatever we do here to change the form will be done by multiplying by
an equivalent of
"one" so that value is not changed. The idea in both the square root
and cube root case is to
figure out what to multiply the denominator by so as to "create" a
perfect square or a
perfect cube, respectively, under the radicals, so that the radical
can then be simplified
"exactly, " thus "removing" the radical. Remember that you must multiply
square root by
square root and cube root by cube root, in order to be able to multiply
the "insides" as desired;
and you must multiply the "top" by the same thing as the "bottom",
so that you have
merely multiplied by "one." |
| 5.3A/249 |
1,7,9,11 |
Simplifying Radicals: Sums with Numbers Only:
You will just be simplifying radicals as in
5.2B, but you will find that the results are just like having "like
terms", like adding 2x + 5x =
7x, except the "x" is a square root or a cube root. |
| WS#5 |
3,8,9,15,17,18,19,23
,30,31,33,51 |
Exact Radical Problems: Practice with
different combinations of operations with roots, but all
the answers are "no radicals." Evaluating "exact radicals" with
variables involved: Here
we are taking square or cube roots of a variable, say x, raised to a
power that will come out of
the radical exactly. The square root of x raised to the n power can be
written as x raised to the
n/2 power; thus if n is an even number, the expression "comes out" of
the radical exactly.
Similarly, the cube root of x raised to the n power is x raised to the
n/3 power, so in the case
that n is a multiple of 3, this expression will "come out" of a cube
root exactly. |
| 5.3B/249 |
27,29,37,55 |
Simplifying Radicals: Algebraic, &
Rationalizing Denominators with Algebraic Square &
Cube Roots: As in the above discussion: When we are faced with the
situation of n not
being the correct multiple to come out of the radical exactly, we pick
the largest integer less
than n that is the correct multiple, then use the exponent rule to
express x raised to the n
power as x raised to this next integer times x raised to whatever is
necessary to "get back up"
to "x to the n" (Example cube root of x raised to the 14th power: The
largest integer less than
14 that is divisible by 3 is 12. Thus x to the 14th = x to the 12th
times x to the 2nd. Cube root
of x to the twelth is excatly x to the 12/3 or x to the 4th, and the x
to the 2nd stays under the
cube root. Same idea as with numbers is used for rationalizing. |
| 5.7/273 |
3,9,13,21,29 |
Scientific Notation |
7.2/357
7.5B/387 |
7,17,25,29,31xxxxxx
xx49 (from 7.5) |
Graphs of Lines: You will have to identify
both x- & y-intercepts. You need to find these points
algebraically .... Not estimating through the graph. You will also have
to find the slope of the
line. You will have to graph 3 points, including the x- & y-intercept.
May use the slope to find
the 3rd point. or "an x, y chart ". Identify equation & slope of
horizontal &vertical lines |
| WS#14 |
1,5,7,8 |
Uses problems in 7.2 to do the following: Putting
equations of lines into Slope-Intercept
form; finding the slope; finding the slope of any
perpendicular line; finding x- and y-intercepts.
Also be able to identify intercepts from a graph as we did on PT#6,
problem
#25. |
| 7.3/364 |
1,5,13 |
Graphs of Linear Inequalities in Two Variables
(Shade Graphs): (Directions will be the
same as on Major Test #3 ... Plot x- & y-intercept (a 3rd point if you
wish to be safer!) for the
line and then show your "Test Point" on the graph and the work for your
"Test" in your problem,
and shade properly.) |
| 7.4/374 |
1,5,9 |
Distance Between Two Points: In words: to
find the distance between two points, do the
following: Take the difference of the "x-values" and then square, do the
same thing for the
difference in the "y-values" then square. Add these two numbers
together, then take the
square root of the result. The formula is on page 366. |
| 7.4/374 |
19,25,27 |
Slope Between Two Points: In words, this
is Rise over Run. Given two points, take the
difference in the "y-values" and divide by the difference in the
"x-values", being careful to keep
the same order (2nd minus 1st) on both top and bottom. The formula is on
page 369. Note:
Also be able to identify slope of a line by looking at its
graph as we did on PT #6, problem
#26 |
| 7.5/386 |
3,11,19,35,39 |
Writing Equations of Straight Lines: (Be
able to put into both Standard Form & Slope -
Intercept Form, depending on which is requested. Use our WS#22
Answers to 7.5 in y=mx+b
form to practice that. |
| PT#6 |
#16 - #19 |
Be able to match the graph of a horizontal or
vertical line to its equation and to identify
its slope as on PT #6. |
| 11.1/602 |
1,3,13,21,23,33,3 |
Systems of Linear Equations (You will need
to know BOTH the Substitution and the
Elimination by Addition Methods) Remember to give your answer as an
ordered pair with the x-value
first and the y-value 2nd. |
Start solving your Algebra Problems
in next 5 minutes!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
Attention: We are
currently running a special promotional offer
for Algebra-Answer.com visitors -- if you order
Algebra Helper by midnight of
January 30th
you will pay only $39.99
instead of our regular price of $74.99 -- this is $35 in
savings ! In order to take advantage of this
offer, you need to order by clicking on one of
the buttons on the left, not through our regular
order page.
If you order now you will also receive 30 minute live session from tutor.com for a 1$!
|
You Will Learn Algebra Better - Guaranteed!
Just take a look how incredibly simple Algebra Helper is:
Step 1
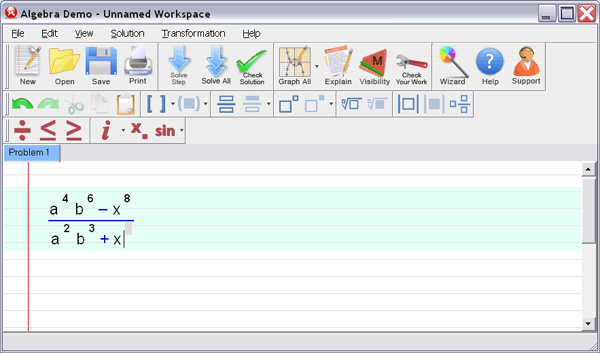
: Enter your homework problem in an easy WYSIWYG (What you see is what you get) algebra editor:
Step 2 :
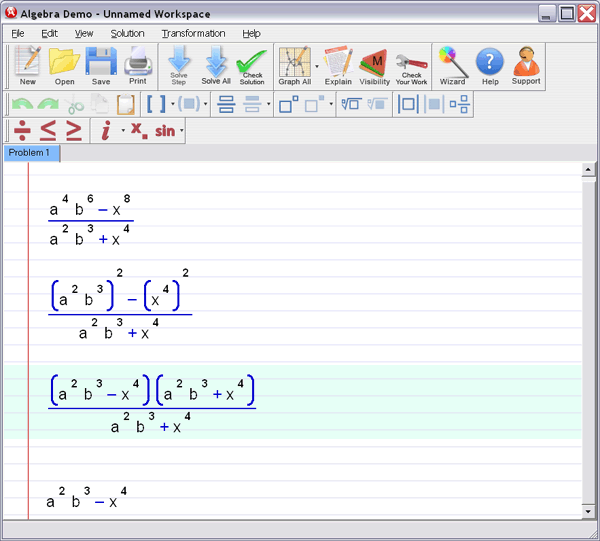
Let Algebra Helper solve it:
Step 3 : Ask for an explanation for the steps you don't understand:
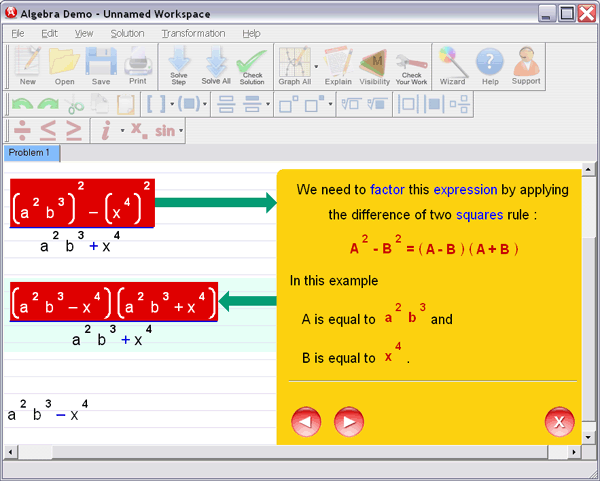
Algebra Helper can solve problems in all the following areas:
- simplification of algebraic expressions (operations
with polynomials (simplifying, degree, synthetic division...), exponential expressions, fractions and roots
(radicals), absolute values)
- factoring and expanding expressions
- finding LCM and GCF
-
(simplifying, rationalizing complex denominators...)
- solving linear, quadratic and many other equations
and inequalities
(including basic logarithmic and exponential equations)
- solving a system of two and three linear equations
(including Cramer's rule)
- graphing curves (lines, parabolas, hyperbolas, circles,
ellipses, equation and inequality solutions)
- graphing general functions
- operations with functions (composition, inverse, range, domain...)
- simplifying logarithms
- basic geometry and trigonometry
(similarity, calculating trig functions, right triangle...)
- arithmetic and other pre-algebra topics
(ratios, proportions, measurements...)
ORDER NOW!
 |
 |
 |
|
Algebra Helper
Download (and optional CD)
Only $39.99
|
|
Click to Buy Now:
OR
|
|
|
 |
 |
 |
|
2Checkout.com is an authorized reseller
of goods provided by Sofmath
|
|
|
 |
| |
| "It
really helped me with my homework. I was
stuck on some problems and your software walked me
step by step through the process..." |
| C. Sievert, KY
| |
| |
 |
| |
Sofmath
19179 Blanco #105-234
San Antonio, TX 78258
|
Phone:
(512) 788-5675
Fax: (512) 519-1805
| | |



