Course Description:
A study of functions, limits, and continuity,
differential calculus of algebraic and
trigonometric functions with applications, and
an introduction to the development of the
definite integral.
Required Text:
Stewart, James (2003). Calculus, (5th ed.),
Belmont, CA: Brooks/Cole, Thomson
Learning, Inc.
Materials: A graphing calculator is required.
Method of Instruction : Lecture
Manuals: None
Disclaimer: None
CORE COURSE PERFORMANCE OBJECTIVES
The student will be able to:
1. Use the concept of functions to solve application problems. (CCC 1,2,6,7)
2. Graph functions to solve mathematical applications. (CCC 2,6,7)
3. Demonstrate understanding of the concepts of limits and continuity. (CCC
1,2,6,7)
4. Use derivatives to solve application problems. (CCC 1,2,6,7)
5. Use integrals to solve application problems. (CCC 2,6,7)
MEASURABLE PERFORMANCE OBJECTIVES
1. Use the concept of functions to solve application problems. (CCC
1,2,6,7)
1.1 Demonstrate understanding of the real number system by solving
problems
using real numbers.
1.2 Solve problems using absolute value.
1.3 Graph and solve problems using functions.
1.4 Solve applications using exponential expressions .
1.5 Demonstrate understanding of the interval notation by using this
notation
for answers to application problems.
1.6 Show understanding of the coordinate plane by solving distance
formula
problems .
1.7 Use the midpoint formula.
1.8 Find the slope and solve problems involving linear relationships .
1.9 Write the equation of a line .
1.10 Solve applications involving parallel/perpendicular lines.
2. Graph functions to solve mathematical applications.
(CCC 2,6,7)
2.1. Show a proficiency in curve sketching through the use of:
a. intercepts
b. symmetry
c. asymptotes
d. domain and range
e. functions/function notation
f. graphing with graphing calculator
2.2 Demonstrate understanding of functions by finding:
a. sum of functions
b. product of functions
c. quotient of functions
d. composition of functions
2.3 Define radians and use them to solve problems.
2.4 Solve applications using right triangle trigonometry.
2.5 Solve basic identities and trigonometric equations.
3. Demonstrate understanding of the concepts of limits and continuity.
(CCC
1,2,6,7)
3.1 Determine the domain and range of a given function.
3.2 Define and use continuity to solve problems.
3.3 Use continuity and limits to sketch curves.
3.4 Evaluate limits.
3.5 Evaluate limits by use of the graphing calculator, intermediate
value
theorem and L'Hopital's rule.
3.6 Solve application problems involving limits.
4. Use derivatives to solve application problems. (CCC 1,2,6,7)
4.1 Find the derivative of an algebraic function by the definition of the
differential.
4.2 Differentiate algebraic functions by means of the product, quotient
and
power rules .
4.3 Find higher order derivatives .
4.4 Find the derivatives of sine and cosine functions.
4.5 Find the instantaneous rate of change of one variable with respect
to
another.
4.6 Differentiate functions by the chain rule.
4.7 Differentiate functions implicitly.
4.8 Solve related rate problems.
4.9 Find the equation of the tangent and normal lines to a curve at a
given
point.
4.10 Find the extreme values of a function by means of the first
derivative
test.
4.11 Determine the intervals of concavity and points of inflection using
the
second derivative test.
4.12 Use the first and second derivative tests to discuss and sketch
algebraic
curves; include the following concepts in curve
sketching:
a. intercepts
b. symmetry
c. asymptotes
d. critical points
4.13 Graph functions, their first and second derivatives on the same
axis.
4.14 Analyze maximum and minimum problems.
4.15 Solve applications problems using the differential.
4.16 Use Newton's method to find roots of an equation .
4.17 Find the rate of change of one variable given the rate of change of
a
related variable and solve related-rate problems.
4.18 Find the differential of logarithmic functions.
5. Use integrals to solve application problems. (CCC
2,6,7)
5.1 Find the antiderivative of a given function.
5.2 Evaluate indefinite integrals using basic formulas.
5.3 Solve velocity and acceleration problems using integration.
5.4 Work gravitational acceleration problems.
5.5 Find definite integrals using the Fundamental Theorem of Calculus
EVALUATION CRITERIA
Students will demonstrate proficiency on all Measurable Performance Objectives
at least to the 75% level. The final grade will be determined using the
College
Grading System:
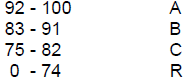
Students should refer to the Student Handbook for
information on
Academic Standing Policy, Academic Honesty Policy, Students
Rights and
Responsibilities and other policies relevant to their academic
progress.
Version Date: 200651
7/5/05



