Derivatives and Tangent Lines

Having discussed in a great amount of detail what a limit is, we return to our original
question: finding the instantaneous rate of change of a function . We previously stated that
the average rate of change of a function over an interval Δx is given by

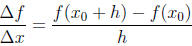
where x₀ is the base point of our interval, and the second point of the interval lies at x₀ + h
(the above formula is called the difference quotient of f at x₀ with increment h, because
it is a quotient of a difference). It is worth returning to the graphical interpretation of the
average rate of change at this point. A line that intersects a curve at two or more points is
called a secant line. In finding the average rate of change between two points of a function,
we are finding the slope of the secant line that intersects those two points.

To find the instantaneous rate of change, we need to look at the average rate of change in
the limit as the length of the interval approaches 0. That is

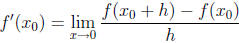
provided that the limit exists. In this situation, the notation f'(x₀) represents the instantaneous
rate of change of the function f(x) at the point x₀. This is a particularly important
quantity in calculus, so we give it a special name - the derivative of f(x) at the point x₀. The
instantaneous rate of change, or derivative, of f(x) at x₀ also has an important graphical
interpretation: f'(x₀) is the slope of the line tangent to f(x) at the point (x₀, f(x₀)). In
this way, we define the line tangent to f(x) at x₀ as the line that passes through the point
(x₀, f(x₀)) with slope f'(x₀). We define the slope of a function f(x) at a point x₀ as the
slope of the tangent line that passes through (x₀, f(x₀)). Now that we have introduced an
extroardinary amount of notation, let us try to get a hold on it by working through some
examples.

Example 1 Let f(x) = x². Find the equation for the secant line passing through (2, f(2))
and (2 + h, f(2 + h). Find the equation for the tangent line passing through (2, f(2)).

Solution In order to find the equation of a line, we need to know either the slope of the
line and a single point the line passes through, or two points on the line, from which we can
calculuate the slope. With this information we can use the point slope form (for a slope m
and point (x₀, y₀))

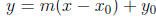
Since we know two points through which the secant line passes, we can find the slope of the
secant line

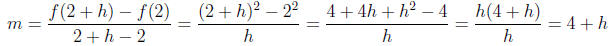
Now using point-slope form, the above slope, and a single point on the line (it is customary
to use the base point of the interval - and there is a good reason for doing so - because we
also want to consider the tangent line at that point) we find

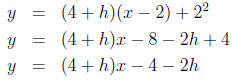
It’s useful to notice what happens as we modify our interval, by manipulating h. When
we extend our interval to the right, by increasing h, the slope increases and the y-intercept
decreases. If we let our interval extend to the left of the base point, by considering negative h
values , the slope decreases and the y- intercept increases . Now let us perform similar analysis
to find the equation of the tangent line (while reusing as much work above as possible).

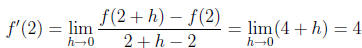
Now we utilize point-slope form once again

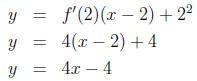
These two equations are very similar; in fact, if we consider the equation for the secant line
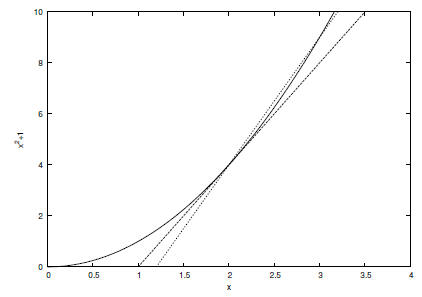
in the limit as h → 0, we arrive at the equation of the tangent line. Graphically, we can see
that as we decrease h, the secant line becomes closer and closer to the tangent line, and in
the limit as h → 0, the secant line is the tangent line. Thus, we can interpret the tangent
line in a slightly different way ; that is, the line tangent to f(x) at x₀ is the secant line with
base point x₀ in the limit as the distance between the two points of the function f(x) the
secant line intersects h → 0.

Example 2 Let f(x) = mx + b be the equation of an arbitrary line. Find the equation of
the line tangent to f(x) at an arbitrary point x₀.

Solution Since the equation of a line passing through a given point is unique, and f(x)
is the unique line of slope m that crosses through every point it does, we suspect that the
tangent line should have to be exactly the line f(x) (and in fact, so should any secant line
passing through the point x₀).

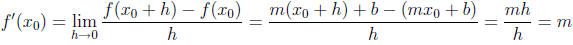
so we see that the slope is exactly the same as the line itself.

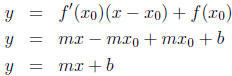
Thus, as suspected, the line tangent to a line at any point is just the line itself.

Example 3 Find the equation of the line tangent to the function f(x) = x³ at x = 0.

Solution We begin as usual by looking at the limit as h → 0 of the difference quotient

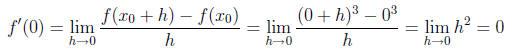
Since this line passes through the point (0, 0), the point-slope equation is very simple

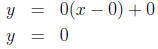
Thus, in this case the tangent line is simply the x -axis. It is noteworthy that this line actually
intersects the function f(x) = x³, which should dispell the myth that a tangent line
cannot cross a function.

Example 4 Find the slope of the line tangent to f(x) = sin(x) at an arbitrary point x.

Solution In finding the derivative of a function at an arbitrary point x, we define a new
function f'(x), which for any x value gives the corresponding value of the derivative at that
point. We call this new function f'(x) the derivative of f. Proceeding with the difference
quotient

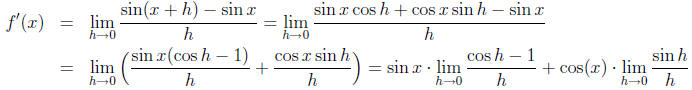
We have already seen that the limit

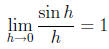
and we can actually use this limit to find the value of the other one using the half angle
formula cos h = 1 − 2 sin²(h/2).

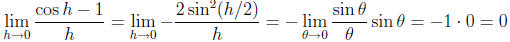
where in the above analysis we substituted h /2 = θ to evaluate the limit. Using these two
limits, we find that

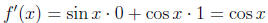
This is a very interesting result. When we look at the rate of change of the function sin(x)
we find that it is the other sinusoidal function cos(x). In fact,

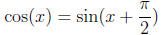
or in other words, the instantaneous rate of change of sin(x) at any point x is simply the
value of sin(x+ π/2), that is, the value of the same function π/2 to the right of the point of
interest. Thus, sin(x) is a function which has rate of change directly related itself.

If we look at the tangent line at x = 2π /3 we find that

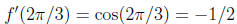
and since

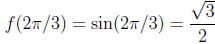
we find the equation for this tangent line as

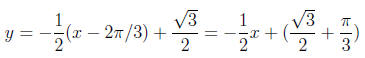
this tangent line will touch the curve at two points, intersecting the curve at one of them.
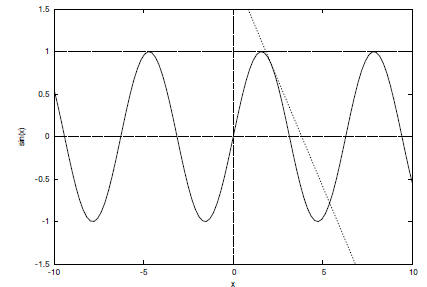
If we consider the tangent line at x = π/2 we have

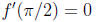
so we have a horizontal line, with equation

y = 1

which touches the curve at an infinite number of points . This should dispell the myth that
a tangent line can only touch a curve in one place, as we have a tangent line that touches
the curve in an infinite number of places.

Since we find the derivative at a point using a limit, it follows that if the limit does not exist,
neither will the derivative, nor a nonvertical tangent line (which will be discussed later). We
say that a function is not differentiable at a point where its derivative does not exist. A
function is not differentiable at any place it has a:

1. corner. Consider f(x) = |x| which has a corner at x = 0. If we look at the secant lines
in the limit as h → 0, we see that from the left side the slope of the tangent line is
approaching −1, and from the right side the slope is approaching 1. Since these limits
do not agree, the derivative and thus tangent line do not exist at x = 0 (a similar
analysis will hold for a corner of any function).

2. a cusp. Consider the function 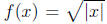at the point x = 0. From the right side
the secant lines approach a vertical tangent line with slope ∞ and from the left side
with slope −∞. Since the limit is increasing or decreasing without bound, it does not
exist, so f(x) is not differentiable at x = 0, the point where it has a cusp.

3. vertical tangent. If the limit of the difference quotient fails to exist because it approaches
∞ or −∞ from both sides, we say that the function has a vertical tangent at
the point of interest (and since ±∞ are not numbers, the derivative does not exist).
An example of function with a vertical tangent is .

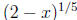4. a discontinuity. If we have a jump discontinuity the secant lines will behave like when
we have a cusp . A function with a jump discontinuity will have different behavior on
both sides of the point of interest. For instance, f(x) = |x|/x, f(0) = 1 has a jump
discontinuity at x = 0. The secant lines approach a horizontal tangent from the right,
and vertical from the left. Thus, the derivative does not exist at this point (nor does
a tangent line).