EXAM 2 – WRITTEN PORTION
Problem 1:
Consider the code scrap shown below:
clc
clear variables
t(1,1) = 0;
n = 1;
dt = 0.2;
while t(n,1) < 0.5
t(n+1,1) = t(n,1) + dt;
n = n+1;
end
After execution of this code,
• What is the value of n ? __________
• What is the value of the final element in the t array? __________
Problem 2:
For each type of problem shown below, we could use either a while…end loop or
a for…end loop.
Circle the type of repetitive structure that would be the most appropriate for
the type of problem.
a. (circle one) while for Countdown from 10 to 0 to initiate a space
shuttle launch.
b. (circle one) while for Calculate a new estimated value of a function
until an error estimate is small enough.
c. (circle one) while for Keep checking for input validity until the
input is within a valid input range.
d. (circle one) while for Record the voltage for 25 sensors, one at a
time.
Problem 3:
A MATLAB program called Main_program and a user-defined function called
plus_times are shown.
% Main_program
% Inputs
x = 5;
y = 2;
% Calculations
[m,n] = plus_times(x,y)
% Outputs
fprintf('x = %2.1f \n', x)
fprintf('y = %2.1f \n', y)
fprintf('m = %2.1f \n', m)
fprintf('n = %2.1f \n', n)
function [x,y] = plus_times(a,b)
% User-defined function that computes
% the sum of the input arguments and
% the product of the input arguments
x = a + b;
y = a * b;
What does the main program print for x, y, m, and n? (Fill in the blanks.)
x = __________
y = __________
m = __________
n = __________
Problem 4:
If we fill a tank that has a leak, the differential equation is
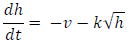
where h is the height of the fluid in the tank, t is time, v is the fill
rate, and k is a discharge coefficient. (v
and k are constants.) Write the appropriate mathematical (not MATLAB) expression
for the Euler’s
method approach to this problem.
Problem 5:
Recall that the quadratic formula solves for the roots of a quadratic
equation (second- order polynomial )
using the formula
.
We expect two answers: x1 and x2. Given this information, the
following user-defined function has been written:
% quadratic.m
% This function computes the roots of a quadratic equation
% of the form (a x^2 + b x + c).
%
% Inputs are a,b,c which are the coefficients of the powers of x.
% Outputs are x1,x2 which are the roots of the equation
%
x1=(-b-sqrt(b^2-4*a*c))/(2*a);
x2=(-b+sqrt(b^2-4*a*c))/(2*a);
a. Based on the function comments and code, write first line of this function
(line 01, the function
definition statement).
b. Write the line of MATLAB code to call this function to solve the quadratic
equation:
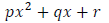
given that the variables p , q, and r are already assigned values in the main
program and that you
wanted to store the roots using variable names root1 and root2.
Problem 6:
Consider the thermocouple problem
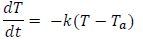
where T is temperature, t is time, and
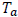and k are constants.
(a) Fill in the blanks in the following code to create a correct MATLAB
implementation of the Euler
solution to the problem . Do not change any of the existing code:
dt=0.001;
k=1.5;
Ta=200;
tmax=5;
n=__________________________
T(1,1)=0;
t(1,1)=0;
while t(n,1) < tmax;
t(n+1,1)=t(n,1)+dt;
T(n+1,1)=__________________________________________________________
n=n+1;
end
plot(t,T)
(b) Now fill in the blanks in this (different but related) code to create a
correct MATLAB implementation
of the Euler solution to the problem. Do not change any of the existing code:
dt=0.001;
k=1.5;
Ta=200;
tmax=5;
n=__________________________
T(1,1)=0;
t(1,1)=0;
while t(n-1,1) < tmax;
t(n,1)=____________________________________________________
T(n,1)=____________________________________________________
n=n+1;
end
plot(t,T)
Problem 7
We wish to write a function for an exact solution of the form
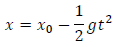
for times between 0 and tmax. Fill in the blanks in this code to create a
correct MATLAB function for
this problem. Do not change any of the existing code.
function [x,t]=Exact(dt,x0,tmax);
g=32.2;
n=1;
x(1,1)=___________;
t(1,1)=0;
while t(n,1) < tmax;
t(n+1,1)=t(n,1)+dt;
x(n+1,1)=x(_______,1)-0.5*g*t(________,1)^2;
n=n+1;
end
EXAM 2 – COMPUTER PORTION
Instructions:
For this portion of the exam you will create two files:
• a main program m-file called lastname_firstname.m
• a function m-file called E_calc_lastname.m
Before beginning the problems, open and save both m-files
now.
Main program
Include your name, section number, and CM number in the header section of your
code.
There should be no output other than what is asked for.
Start problem 1 in this file with the lines:
%% Problem 1
clc
clear variables
close all
Start problem 2 in this file with the line (clear only the
variables):
%% Problem 2
clear variables
Function
Include your name, section number, and CM number in the header section of your
function. There should be no output other than what is asked for.
Problem #1 (20 pts)
Recall that, in MATLAB, we can define an array A with the
following command:
A = [2; -5; -3; 6; 8; 9; 2; -7; 1; -9];
• Type the array A into your main program after the
comment line %% Problem 1.
• Write a program that counts the number of negative numbers in this array.
• Display this count (a single integer answer) on screen.
Problem #2 (40 pts)
• Download the EXCEL file named curve_fit.xls from
the course web page at
• Save the EXCEL file in the same directory as your Exam 2 m-files.
• Begin this section of code after the comment line %% Problem 2.
The EXCEL spreadsheet contains two columns of data
recorded by a pressure transducer during
a calibration procedure. The first column is the voltage (in mV) and the second
column is the
corresponding pressure (in kPa).
(a) Start this section of your code with the comment line:
% Part (a).
• Read in the data and plot pressure (y axis) as a function of voltage (x axis).
• Use descriptive axis labels and a descriptive title for your plot.
• Plot these data using data symbols with no connecting lines.
(b) Start this section of your code with the comment line:
% Part (b).
Your supervisor believes that the relationship between pressure and voltage is
linear, that is,
P = aV
• Create a line of this form, with a = 1.2, and add it to
your data plot from part (a).
• Plot this line as a solid line with no additional data symbols.
• If you cannot get this portion to work correctly, we suggest that you skip to
part (c).
(c) Start this section of your code with the comment line:
% Part (c).
The total error (E) between the line and the data can be written as
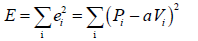
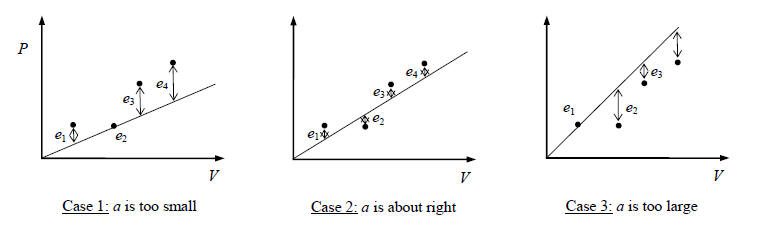
where i = 1…n and n is the total number of data points. If
the slope a is too small (Case 1 in the
figures), the error is large. If a is too large (Case 3) the error is also
large. If a is just right (Case
2), the total error will be small.
Write the function called E_calc_lastname.m that
• accepts as inputs: proposed slope a, the pressure array P, and the voltage
array V,
• uses a and the elements of the P and V arrays to compute the total error E
given by
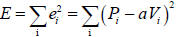
• returns the value of E to the main program.
Test your function from the main program by
• Setting a = 0.5, 1.2, and 2.0
• Print the result E to the screen with appropriate words using an fprintf
statement, for
example:
a=0.50 E= X.XXXXXe+XXX
a=1.20 E= X.XXXXXe+XXX
a=2.00 E= X.XXXXXe+XXX
