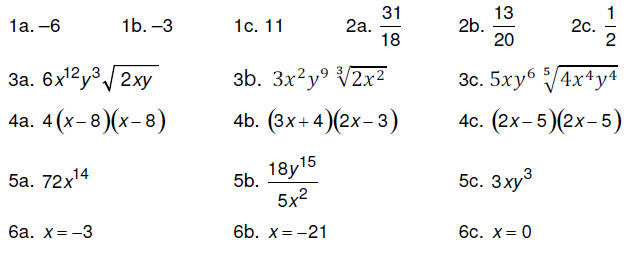This test is designed to give you and your instructors an
idea of your level of skill in doing high school
algebra as you begin Math 1155. You should have been able to do these problems
correctly and with
little difficulty. If you are really lost doing these problems you should talk
to Jessica or Michelle.
Go through the solutions to the problems and be sure you
understand how to do them.
1. Simplify:
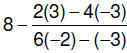
Follow the order of operations for simplifying arithmetic
expressions:
Step 1 Simplify expressions inside grouping
symbols, which include parentheses ( ), brackets [ ],
the fraction bar -> a/b absolute value bars | |, and radicals
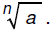
Step 2 Simplify exponents, square roots, and
absolute values.
Step 3 Simplify multiplication and division, working left to right.
Step 4 Simplify addition and subtraction, working left to right.
Practice problems: Simplify each of the following.
Check the answers at the end of this document.
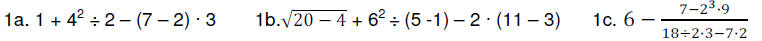
2. Simplify:
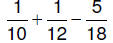
Step 1 Find the Least Common Denominator (LCD) by
prime factoring each denominator and then
multiplying the largest group of each prime factor.
10 = 2 • 5
12 = 2 • 2 • 3
18 = 2 • 3 • 3
Largest group of 2's is 2 • 2 (in 12)
Largest group of 3's is 3 • 3 (in 18)
Largest group of 5's is 5 (in 10)
So, the LCD = 2 • 2 • 3 • 3 • 5 = 180
Step 2 Convert each given fraction into an
equivalent fraction with the LCD as the denominator.
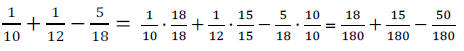
Step 3 Now that the fractions have the same
denominator, add or subtract the numerators.
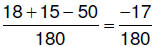
Step 4 Reduce by canceling factors common to the
numerator and denominator.
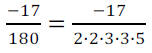
Since there are no factors common to the numerator and
denominator the fraction cannot be
reduced . The final answer is 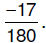
Practice problems: Simplify each of the following.
Check the answers at the end of this document.
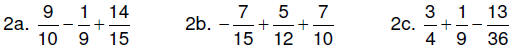
3. Simplify:
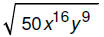
Factor the radicand. Each pair of identical factors is a
perfect square and so that factor will come
out from under the radical. Any left over single factors will remain under the
radical.
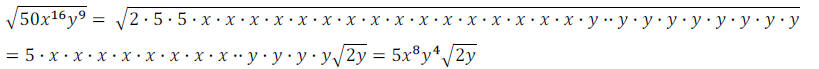
Rather than writing out all the factors of x and y, we
could simply divide their exponents by the
index of the radical, which is 2 since we have a square root . The resulting
quotient is the exponent
of the variable outside the radical and the resulting remainder is the exponent
of the variable under
the radical.
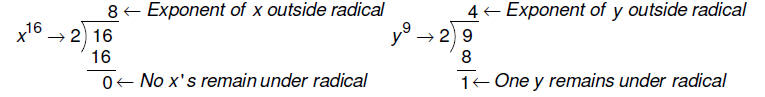
Practice problems: Simplify each of the following.
Check the answers at the end of this document.
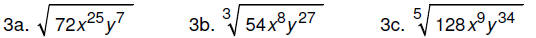
4. Factor: 2x^2 + 5x − 12xxx
We are going to do a LOT of factoring in this course. Here
is a general procedure to follow:
Step 1 Factor out the Greatest Common Factor (GCF).
For example, factor: 
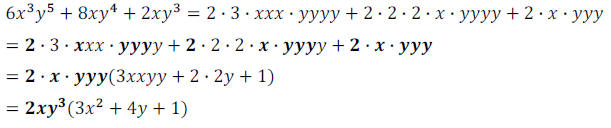
The GCF is 2xy^3 . Notice the third term, 1, must be there
for the factorization to be correct.
Step 2 Count the number of terms and look for
factoring patterns.
Two terms: Try factoring using one of these
patterns (memorize these!)
• Difference of perfect squares:
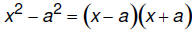
• Difference or sum of perfect cubes:
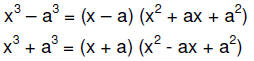
Notice the only difference between the above two formulas
are the signs .
Three terms:
• Try factoring using the patterns for perfect square
trinomials:
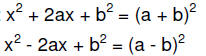
Notice the only difference between the above two formulas
are the signs.
• If the trinomial has the form x^2 + bx + c , find two
integers whose product is c and whose sum
is b. Let's say the integers are m and n. Then x^2 + bx + c = (x + m)(x + n).
For example, factor: x^2 + x − 12
We need two integers whose product is –12 and whose sum is 1. Integer factors of
12 are
1•12, 2•6, and 3•4. Since the product is negative, the two factors must have
different signs.
Since the sum must be 1, we choose –3•4.
Thus,
x^2 + x − 12 = (x − 3)(x + 4).
• If the trinomial has the form ax^2 + bx + c , find two
integers whose product is a•c and whose
sum is b, replace the bx term using these integers, and factor by grouping. For
an example,
see below.
Four terms: Try factoring by grouping.
For example, factor: 5x^2 + 15x − 2xy − 6y
Group the first pair of terms and factor out the GCF; do the same for the second
pair of terms.
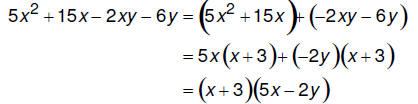
Step 3 Factor completely. In some cases, it may be
necessary to factor more than once.
Remember that multiplication can be used to check the factorization.
Now, let's factor 2x^2 + 5x − 12:
Step 1 GCF: There is no factor common to all the terms so there is no GCF other
than 1 or –1.
Step 2 Number of terms: There are three terms and they
match the pattern ax^2 + bx + c , where a = 2,
b = 5, and c = –12. So, we find two integers whose product is a•c = 2•(–12) =
–24 and whose sum
is b = 5. Here are the possibilities for 24 (ignore the sign for the moment):
24 = 1•24, 2•12, 3•8, 4•6
The pair that can have a sum of 5 is 3•8 if we attach a
negative sign to the 3. The integers we seek
are –3 and 8 since (−3)(8)= −24 and −3 + 8 = 5 .
Replace the middle term, 5x, with its equivalent –3x + 8x
and factor by grouping:
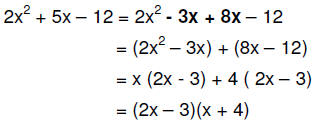
Step 3 Factor completely: Since the expression
cannot be further factored the answer is (2x − 3)(x + 4).
Practice problems: Factor each of the following.
Check the answers at the end of this document.
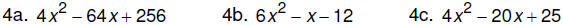
5. Simplify:
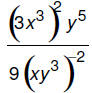
Be sure you have memorized the laws of exponents :
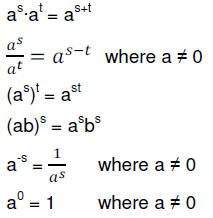
It usually is easiest to simplify the numerator and
denominator individually and then simplify the
quotient.
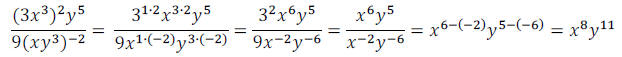
Practice problems: Simplify each of the following.
Check the answers at the end of this document.
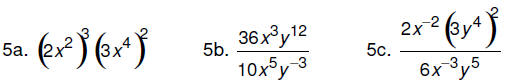
6. Solve: 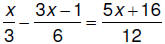
When solving an equation that contains fractions, it
usually is easiest if you clear the fractions first
by multiplying each term by the LCD of all the terms. The LCD of 3, 6, and 12 is
12, so multiply
each term by 12 and then simplify.
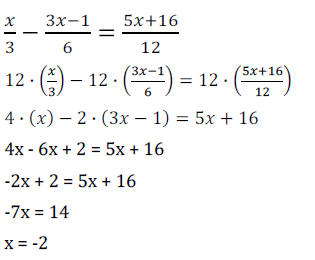
Practice problems: Solve each of the following.
Check the answers at the end of this document.

7. Graph the line : y = - 2/3 x + 5
The slope of the line is - 2/3 and the y-intercept is 5.
To graph the line, start at the point (0,5) and
then go down 2 and to the right 3 repeatedly, plotting points as you go along.
Answers to practice problems: