1 Arnoldi/Lanczos Iterations
Krylov Subspace Methods
•Given A and b, Krylov subspace
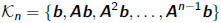
| |
linear systems |
eigenvalue problems |
| Hermitian |
CG |
Lanczos |
| Nonhermitian |
GMRES, BiCG, etc. |
Arnoldi |
Arnoldi Algorithm
•Let 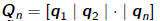 be m n matrix with first n columns of Q
be m n matrix with first n columns of Q
and 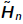 be (n + 1) x n upper-left section of H
be (n + 1) x n upper-left section of H
•Start by picking a random q1 and then determine q2and
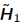
•The nth columns of AQn = Qn+1 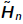 can be written as
can be written as
Aqn = h1nq1 + + hnnqn + hn+1;nqn+1
•Algorithm: Arnoldi Iteration
given random nonzero b, let 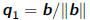
for n = 1 to 1, 2, 3,.....
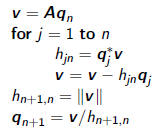
Lanczos Iteration for Symmetric Matrices
•For symmetric A, 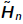 and Hn are tridiagonal,
denoted by
and Hn are tridiagonal,
denoted by 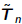 and Tn,
and Tn,
respectively. AQn = Qn+1 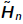 can be written as three- term recurrence
can be written as three- term recurrence
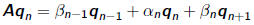
•where 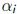 are diagonal entries and
are diagonal entries and
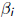 are sub-diagonal entries of
are sub-diagonal entries of
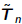
•Algorithm: Lanczos Iteration
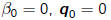
given random b, let 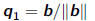
for n = 1 to 1,2,3,....
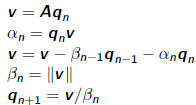
Question: What are the meanings of 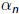 and
and 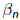 in
in 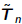 ?
?
Properties of Arnoldi and Lanczos Iterations
•Eigenvalues of Hn (or Tn in Lanczos iterations) are called Ritz values.
•When m = n, Ritz values are eigenvalues .
•Even for n << m, Ritz values are often accurate approximations to
eigenvalues of A!
•For symmetric matrices with evenly spaced eigenvalues, Ritz values
tend to first convert to extreme eigenvalue.
•With rounding errors, Lanczos iteration can suffer from loss of
orthogonality and can in turn lead to spurious “ghost” eigenvalues.
Arnoldi and Polynomial Approximation
•For any
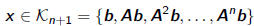
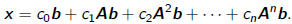
•It can be interpreted as a polynomial in A times b , x = p(A)b, where
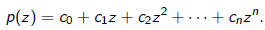
•Krylov subspace iterations are often analyzed in terms of matrix
polynomials.
•Let Pn be the set of polynomials of degree n with cn = 1.
•Optimality of Arnoldi/Lanczos approximation: It finds
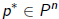 s.t.
s.t.
•p* is optimal polynomial among
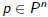 that minimizes
that minimizes
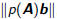 ,
,
which is equivalent to minimizing the distance betwen Anb and its
projection in Kn
•p* is the characteristic polynomial of Hn
Ritz values are the roots of an optimal polynomial
2 Conjugate Gradient Method
Krylov Subspace Algorithms
•Create a sequence of Krylov subspaces for Ax = b
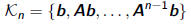
and find an approximate (hopefully optimal) solutions x n in Kn
•Only matrix-vector products involved
•For SPD matrices, most famous algorithm is Conjugate Gradient (CG)
• method discovered by Hestenes/Stiefel in 1952
•Finds best solution 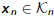 in norm
in norm
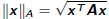
•Only requires storing 4 vectors (instead of n vectors) due to three-term
recurrence
Motivation of Conjugate Gradients
•If A is m x m SPD, then quadratic function
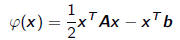
has unique minimum
• Negative gradient of this function is residual vector
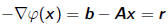
so minimum is obtained precisely when Ax = b
•Optimization methods have form
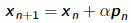
where pn is search direction and 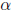 is step length chosen to minimize
is step length chosen to minimize
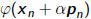
• Line search parameter can be determined analytically as
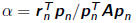
•In CG, pn is chosen to be A-conjugate (or A-orthogonal) to previous
search directions, i.e., 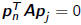 for j < n
for j < n
Conjugate Gradient Method
| Algorithm: Conjugate Gradient Method |
|
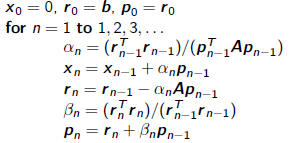 |
step length
approximate solution
residual
improvement this step
search direction |
•Only one matrix-vector product Ap n-1 per iteration
•Apart from matrix-vector product, operation count per iteration is
O(m)
•If A is sparse with constant number of nonzeros per row, O(m)
operations per iteration.



