Chapter 12
Make Your Own Functions: Inline
and M- les
As you use Matlab to solve problems you will probably want
to build your own Matlab
functions. You can do this either by putting simple expressions into your code
by using
Matlab's inline command, or by defining function les with .m extensions called
M- les.
12.1 Inline Functions
Matlab will let you define expressions inside a script for use as functions
within that script
only. For instance, if you wanted to use repeated references to the function
you would use the following syntax (to make both a line plot in x with y = 2 and
to make
a surface plot):
| Example 12.1a (ch12ex1a.m)
% Example 12.1a
clear;close all;
f=inline('sin(x.*y)./(x.^2+y.^2)','x','y');
x=-8:.1:8;y=x;
plot(x,f(x,2))
[X,Y]=meshgrid(x,y);
figure
surf(X,Y,f(X,Y)) |
The expression that defines the function is in the first
string argument to inline and the
other string entries tell inline which argument goes in which input slot when
you use the
function.
12.2 M- le Functions
M- le functions are subprograms stored in text les with .m extensions. A
function is
different than a script in that the input parameters it needs are passed to it
with argument
lists like Matlab commands (think about sin(x) or plot(x,y,'r-')). Note,
however, that
the variables inside Matlab functions are invisible in the command window. So to
debug a
function you need to use print and plot commands in the function le. Or you can
make it
a stand-alone script by commenting out the function line so that its variables
are available
at the Matlab command level.
You can also pass information in and out of functions by
using Matlab's global command
to declare certain variables to be visible in all Matlab routines in which the
global
command appears. For instance, if you put the command
global a b c;
both in a script that calls derivs.m (see below) and in
derivs.m itself, then if you give a,
b, and c values in the main script, they will also have these values inside
derivs.m. This
construction will be especially useful when we use Matlab's differential
equation solving
routines in Chapter 16.
Rather than give you a syntax lecture we will just give
you three useful functions as
examples, with comments about how they work.
12.3 Derivative Function derivs.m
The first is a function called derivs.m which takes as input a function
array y representing
the function y(x), and dx the x-spacing between function points in the array. It
returns yp
and ypp, numerical approximations to the first and second derivatives, as
discussed in the
section on numerical differentiation. First we will give you the script, then we
will show
you how to use it.
| Example 12.3a (derivs.m)
% Example 12.3a
function [yp,ypp]=derivs(y,dx)
%*********************************************************
% This function numerically differentiates the array y which
% represents the function y(x) for x-data points equally spaced
% dx apart. The first and second derivatives are returned as
% the arrays yp and ypp which are the same length as the input
% array y. Either linear or quadratic extrapolation is used
% to load the derivatives at the endpoints. The user decides
% which to use by commenting out the undesired formula below .
%*********************************************************
% load the first and second derivative arrays
at the interior points
N=length(y);
yp(2:N-1)=(y(3:N)-y(1:N-2))/(2*dx);
ypp(2:N-1)=(y(3:N)-2*y(2:N-1)+y(1:N-2))/(dx^2);
% now use either linear or quadratic
extrapolation to load the
% derivatives at the endpoints
% linear
%yp(1)=2*yp(2)-yp(3);yp(N)=2*yp(N-1)-yp(N-2);
%ypp(1)=2*ypp(2)-ypp(3);ypp(N)=2*ypp(N-1)-ypp(N-2);
% quadratic
yp(1)=3*yp(2)-3*yp(3)+yp(4);yp(N)=3*yp(N-1)-3*yp(N-2)+yp(N-3);
ypp(1)=3*ypp(2)-3*ypp(3)+ypp(4);ypp(N)=3*ypp(N-1)-3*ypp(N-2)+ypp(N-3);
|
To use this function you can use the following script
| Example 12.3b (ch12ex3b.m)
% Example 12.3b (Physics 330)
% First build an array of function values
x=0:.01:10; y=cos(x);
% Then, since the function returns two arrays
in the form
% [yp,ypp], you would use it this way:
[fp,fpp]=derivs(y,.01);
% look at the approximate derivatives
plot(x,fp,'r-',x,fpp,'b-')
title('Approximate first and second derivatives') |
Note that we didn't have to call them [yp,ypp] when we
used them outside the function
in the main script. This is because all variables inside functions are local to
these programs
and Matlab doesn't even know about them in the command window.
Sorry, we lied-we need to bore you with some syntax
because everybody gets confused
about the first line in a function program. The syntax of the first line is this
function output=name(input)
The word function is required. output is the thing the
function passes back to whomever
called it and its name is local to the function. If it is a single variable name
then the code
in the function needs to assign that variable name a value, an array of values,
or a matrix of
values. If the function returns more than one such result then the names of
these results are
put in square brackets , as in derivs.m. The function returns these results to
the assigned
variable(s), as in the derivs example:
[fp,fpp]=derivs(y,dx);
The keyword name in the function command line above should
be the name of the .m le
that contains the function code. (You can use other names, but you might drive
yourself
nuts if you do.) input is the argument list of the function. When the function
program
is called the arguments passed in and the arguments used in the function must
match in
number and type .
12.4 Definite Integral Function defint.m
This function uses the midpoint rule to integrate a function over a chosen
interval using a
chosen number of integration points. The function to be integrated must be coded
in the
sub function contained at the end of the function le defint.m (Note: Matlab's
quad and
especially quadl do the same thing, only better. This is just a simple example
to show you
how to program.)
| Example 12.4a (defint.m)
% Example 12.4a (Physics 330)
function s=defint(a,b,N)
%*********************************************************
% this function uses the midpoint rule on N subintervals
% to calculate the integral from a to b of the function
% defined in the sub function at the bottom of this
% function
% load dx and build the midpoint rule x-values
%*********************************************************
dx=(b-a)/N;
x=a+.5*dx:dx:b-.5*dx;
%*********************************************************
% use the function f(x) defined in the sub function below
% to obtain the midpoint approximation to the integral and assign
% the result to s
%*********************************************************
s=sum(f(x))*dx;
% here's the sub function
function y=f(x)
% define the function f(x) and assign it to y
y=cos(x);
%end defint.m |
To use it, first edit the file defint.m so that the sub function at the bottom of
the le
contains the function you want to integrate. Then give defint.m the integration
limits (say
a = 0 and b = 1) and the number of points N = 1000 to use in the midpoint rule
like this
defint(0,1,1000)
or
s=defint(0,1,1000);
In the first case the approximate integral prints on the screen; in the second it
doesn't print
but is assigned to s.
12.5 Indefinite Integral Function indefint.m
This function takes an array of function values in y and an x-spacing dx and
returns an
approximate indefinite integral function
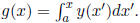The function values must start
at x = a and be defined at the edges of the subintervals of size h rather than at
the centers
as in the midpoint method . Because of this we have to use the trapezoid rule
instead of the
midpoint rule. The trapezoid rule says to use as the height of the rectangle on
the interval
of width h the average of the function values on the edges of the interval:
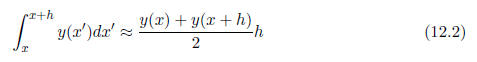
Note that this function does exactly the same thing as Matlab's function
cumtrapz.
| Example 12.5a (indefint.m)
% Example 12.5a (Physics 330)
function g=indefint(y,dx)
%*********************************************************
% returns the indefinite integral of the function
% represented by the array y. y(1) is assumed to
% be y(a), the function value at the lower limit of the
% integration. The function values are assumed to be
% values at the edges of the subintervals rather than
% the midpoint values. Hence, we have to use the
% trapezoid rule instead of the midpoint rule:
%
% integral(y(x)) from x to x+dx is (y(x)+y(x+dx))/2*dx
% The answer is returned as an array of values defined
% at the same points as y
%*********************************************************
% the first value of g(x) is zero because at this first value
% x is at the lower limit so the integral is zero
g(1)=0;
N=length(y);
% step across each subinterval and use the trapezoid area
% rule to find each successive addition to the indefinite
% integral
for n=2:N
% Trapezoid rule
g(n)=g(n-1)+(y(n-1)+y(n))*.5*dx;
end |
Take a minute now and use derivs.m and indefint.m to make overlaid plots of the
function f(x) = cos xe -x, its first and second derivatives, and its indefinite
integral F(x) = x
on the interval x = [0, 3].
