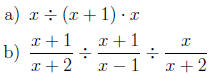Math 1010 Exam 3 Review Sheet

1. [6.5, 6.6] Solve by completing the square
and by using the quadratic formula .
Give all solutions, including complex
number solutions . On the exam, there
will be some problems where you will be
asked to complete the square. On others,
you may be asked to use the quadratic
formula.

a) x² + 2x − 2 = 0
b) 2x² + 5x −4 = 0
c) 2x² − 4x + 3 = 0
d) 4x² − 20x + 25 = 0

2. [6.6] Without solving the equation, determine
if the the solution set consists of
two rational numbers, two real numbers
that are not rational , one real number,
or two complex numbers .

a) 12x² + 3x = 2
b) 2x² − 6x − 56 = 0
c) 4x² + 4x + 1 = 0
d) 5x² + 10x + 6 = 0

3. [6.6] Give the derivation of the quadratic
formula. In other words, start with ax²+
bx + c = 0 and solve.

4. [6.7] Solve the equations.

a)
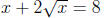
b) x⁴ − 3x² + 2 = 0
c)
d)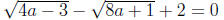

5. [7.1] Match the graphs with the functions .

f(x) = (x + 1)²
g(x) = (x − 1)²
h(x) = x² + 1
k(x) = x² − 1

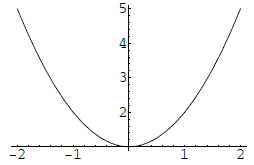
a)

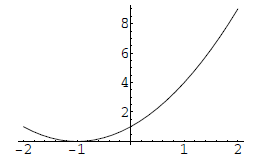
b)

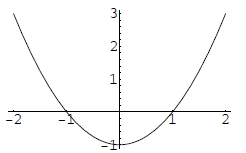
c)

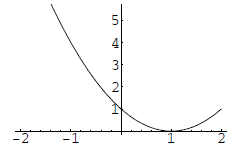
d)

6. [7.2] Explain in words how the graphs of
y = x² and f(x) = a(x − h)² + k are
related. In particular, point out the role
played by each of the numbers a, h, and
k.

7. [7.2] Identify the vertex and the line of
symmetry for the graphs of the quadratic
functions. Then sketch their graphs.

a) f(x) = 3x² − 12x + 7
b) g(x) = x² + 3x + 1
c) w(x) = 4+2x − x²

8. [7.2] Find the maximum value of the
function f(x) = 3 − 4x − x². (In other
words, find the largest possible value
for f(x).) Does f(x) have a minimum
value?

9. [7.3] Find the minimum value of the
function f(x) = 1+6x + x². Does the
function have a maximum value?

10. [7.2] A fence is to be built along the side
of a very long barn to create a hog pen.
There is 240 feet of fence avialable to
build three sides of the pen and the barn
will serve as the other side. What should
the dimensions of the pen be in order to
make the pen as large as possible?

11. [8.1] Find the domain of the functions.

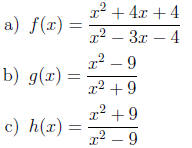
12. [8.1] Reduce the rational functions to
lowest terms .

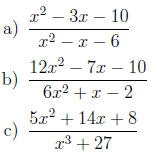
13. [8.1] Explain why the functions f(x) =
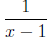and 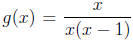are not the
exact same functions.

14. [8.2] Multiply or divide the rational functions
and simplify the answer .

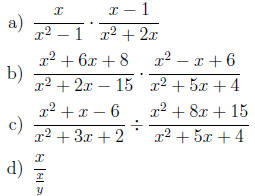
15. [8.3] Add or subtract the rational functions
as indicated. Simplify your answer.

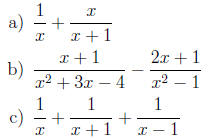
16. [8.3] Compute and simplify.