MATH 121 FALL 2008 TEST 4 SOLUTIONS

1. A function f is defined by the rule f(x) = −7x² + bx + c, but we do not know
what the values b and c are . Select the correct statement from the four statements
below:
(1) The function has both a minimum and a maximum
(2) The function has a minimum but no maximum
(3) The function has a maximum but no minimum
(4) The function has neither maximum nor minimum
The leading coeffient is negative so the graph opens downward and has a maximum.
It has no minimum.

2. Write each quadratic function in the form y = a(x − h)² + k
(1) y = 2x² − 12x + 22

Use the method of completing the square:
y = 2x² − 12x + 22
= 2(x² − 6x) + 22
= 2(x² − 6x + 9 − 9) + 22
= 2(x² − 6x + 9) − 18 + 22
= 2(x − 3)² + 4

(2) y = −3x² + 6x − 3
Complete the square:
y = −3(x² − 2x + 1)
= −3(x − 1)²

3. Find the vertex of each of the following quadratic functions:
(a) f(x) = −3(x − 5)² + 7
The vertex is at (5, 7).

(b) f(x) = 3x2² − 12x + 1

Complete the square:
f(x) = 3(x² − 4x) + 1
= 3(x²− 4x + 4 − 4) + 1
= 3(x² − 4x + 4) − 12 + 1
= 3(x − 2)² − 11
The vertex is at (2,−11).

3. Let f(x) = −3x² − 9x + 4. Find the range of this function, the maximum or
minimum value of the function, and identify the intervals on which the function is
increasing or decreasing.
Complete the square:


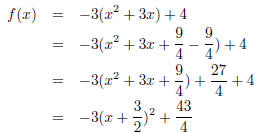
We now observe that this is a parabola with maximum at 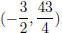; the range of
the function is 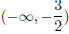, the function is increasing on 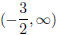, and decreasing
on .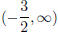

4. Solve the inequality .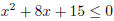

This quadratic factors as
(x + 5)(x + 3)

so it has roots at x = −5 and x = −3. The parabola opens upward, so its graph will
be below the x axis between the two roots . Therefore the solution set is [−5,−3].

5. Solve the inequality.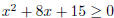
This is the same quadratic as in the previous problem . Therefore, the graph will
be above the x axis on the intervals 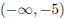and .

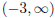6. Mike wants to wants to enclose a rectangular area for his rabbits alongside his
large barn using 30 feet of fencing. What dimensions will maximize the area fenced
if the barn is used as one side of the rectangle?

Let w be the width and L be the length. Then
2w + L = 30,
and the area is given by wL = w(30 − 2w). The area is a quadratic with zeros at
w = 0 and w = 15.. That means that the vertex of the parabola and hence its
maximum occurs at the midpoint between the zeros, which is w =15/2. The length
L = 30 − 2(15/2) = 15.

7. Find the quotient and the remainder when x⁴ − 3x² + 6 is divided by x² − 4.


8. Use synthetic division to find the quotient and remainder when −3x³ + 5x² + 1
is divided by x + 5.


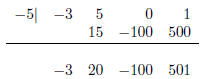
The quotient is −3x² + 20x − 100, and the remainder is 501.

9. Use synthetic division to evaluate the value g(−2) when g(x) = x³ − 7x + 2.


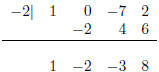
10. Use the rational zero theorem to find all possible rational zeros for the polynomial
2x³ − 5x² − 4x + 3.

All possible rational zeros are all possible factors of 3 divided by all possible factors
of 2. They are


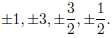
11. Find all real and imaginary zeros of the polynomial w⁴ + w³ − w² + w − 2.
By the rational zeros theorem, the possible roots are
±1,±2.

Using synthetic division


Use synthentic division a second time:


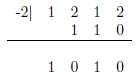
The quotient is now x² + 1, which has roots ±i. Therefore, all roots are 1,−2,±i.

12. Find the product by multiplying:
(1) [x − (3 + 2i)][x − (3 − 2i)]

Use the difference of two squares formula to simplifty the multiplication :




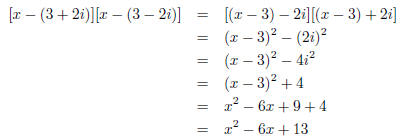
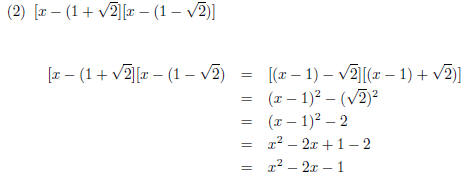
13. If y varies directly as x, and y = 9 when x = 2, what is y when x = −3?
Let y = kx. Then 9 = k(2), so k =9/2. This means that y =9/2 x. When x = −3, we
have y =.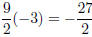

14. Find a polynomial with real coefficients that has the given roots:

(a) 4 + i
By the conjugate pair theorem, a polynomial that has 4 + i as a root
must also have 4 − i as a root. One such polynomial is

(x − [4 + i])(x − [4 − i]).
Using the difference of two squares:



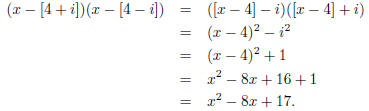
(b) 3, 1 − i.
By the conjugate pairs theorem, such a polynomial must have 1+i as a
root. One such a polynomial is
(x − 3)(x − [1 − i])(x − [1 + i]).

Again, we can multiply this out with the aid of the difference of two
squares formula:


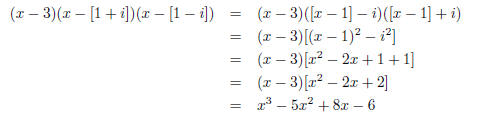
15. Solve the equation


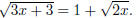
Square both sides, rearrange, and square both sides again to get rid of radicals :


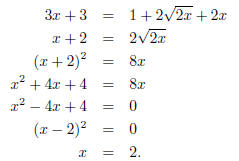
16. Solve the equation (x² + x)² − 8(x² + x) + 12 = 0.
Put u = x² + x. Then
u² − 8u + 12 = 0
which factors as
(u − 6)(u − 2) = 0.
This in turn leads to
u = 6 and u = 2
so that we have the two equations
x² + x = 6 and x² + x = 2.
Solving these last two quadratic equations by factoring , we see that the solutions
are
x = −3, x = 2, x = −2, x = 1.

17. Solve the equation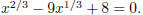
Put u = x^1/3. Then the equation becomes
u² − 9u + 8 = 0
which factors as
(u − 8)(u − 1) = 0
giving answers of
u = 8 and u = 1.
This means that x^1/3 = 8, so that x = 8³ = 512. It also means that x^1/3 = 1, so
that x = 1. The answers are x = 1 and x = 512.

18. Solve the equation |x² − 6| = 5x
Either x² − 6 = 5x or x² − 6 = −5x.
We get
x² − 6 = 5x
x² − 5x − 6 = 0
(x − 6)(x + 1) = 0
so that x = 6 or x = −1. We also have
x² − 6 = −5x
x² + 5x − 6 = 0
(x + 6)(x − 1) = 0
so that x = −6 or x = 1. Thus the answers are x = 6,−6, 1,−1..