Common aspects of professional development:
Teaching Communities in Elementary and Intermediate Algebra met weekly for a
year with similar focus:
• Design backwards from Student Learning Outcomes
• Develop common final exam questions aligned with SLOs
• Develop learning activities to foster achievement of SLOs
Contrasting aspects of the professional development:
| |
Elementary Algebra |
Intermediate Algebra |
Development
and use of
learning
activities |
Individual instructors developed
and shared activities; participants
used what appealed to them;
activities posted on Bb |
Instructors identified gaps in their texts
relative
to SLOs, individual instructors wrote problems to
address SLOs, editor pulled problems into an
activity that was used by all; a coherent packet of
27 activities |
| Follow-up |
Well-attended monthly retreats;
instructors chose focus for the
semester, e.g. CAI, discussion of
NRC’s How Students Learn Math
in the Classroom, mastery
quizzes |
Pre-semester assessment of final exams with
instructors who had just taught the course and
those planning to teach the course; revision of
activities based on assessment results and
instructor feedback; production of a packet for
sale in the bookstore. |
Impact on learning:
Based on an analysis of a random sample of final exams across sections
| Percent proficient or better |
| |
FA
03
N=23 |
FA 06
N=36 |
| Communication |
57% |
39% |
| Problem-solving |
39% |
39% |
| Multiple-Reps |
61% |
32% |
| Percent proficient or better |
| |
FA
04
N=32 |
SP
05
N=30 |
FA 05
N=32 |
SP 06
N=28 |
| Communication |
81% |
77% |
83% |
82% |
| Problem-solving |
69% |
73% |
90% |
89% |
| Multiple-Reps |
59% |
80% |
80% |
82% |
Plausible factors contributing to improvements or
declines in learning:
| |
Elementary Algebra |
Intermediate Algebra |
Planning
Analysis of activities;
% of instructors using
activities or other
materials aligned with
SLOs |
75% of TC activities focused on
Skills SLO. FA 06 assessment: 33%
of instructors submitting student work
used TC activities; weak alignment of
other instructional materials with
these 3 SLOs |
Communication, PS, and MR integrated
throughout all activities.
For each final exam assessment 100%
of instructors submitting student work
used TC activities; strong alignment of
texts/CAI with these 3 SLOs |
Teaching
Analysis of exams;
Instructor reflection |
Weak alignment of exams with SLOs;
only a few instructors using TC
exams. Instructors reported not
knowing how to incorporate TC
activities into their class. |
Instructors reported in each assessment
that at least 50% of class time devoted
to TC activities |
Next steps :
SP 07: Retreats for Elementary Algebra instructors focused on pedagogy that
promotes problem-solving
SU 07 : Feedback from recent Elementary Algebra retreats and assessment results
used to develop a new
set of class activities with an accompanying instructors’ manual
FA 07: “Users” group will meet weekly to conduct a pared-down version of the
Japanese Lesson Study
Los Medanos College
Developmental Math Program’s Student Learning Outcomes
1. Communication Outcome: Students will read, write, listen to, and speak
mathematics with understanding:
2. Problem Solving Outcome: Students will use mathematical reasoning to
solve problems and a
generalized problem solving process to work word problems.
3. Multiple Representations Outcome: Students will demonstrate the
ability to use verbal, graphical,
numerical , and symbolic representations of mathematical ideas.
4. Applications Outcome: Students will recognize and apply math concepts
in a variety of relevant settings
and demonstrate the math skills and knowledge necessary to succeed in subsequent
courses.
5. Effective Learner Outcome: Students will demonstrate the
characteristics of an effective learner.
Sample problems aligned with these SLOs 1-3 above:
Elementary Algebra
1. On January 1, 2008, the minimum wage in California is increasing to $8.00 an
hour. The federal government
defines a family of four as “ low income ” if they make $30,975 or less a year. A
man and a woman living in
California with two children both earn this new minimum wage and work full-time.
Are they considered “low
income” by the federal government? Support your answer with clear mathematical
reasoning. (If you don’t have all
of the information you need, describe assumptions you are making in order to
work the problem.)
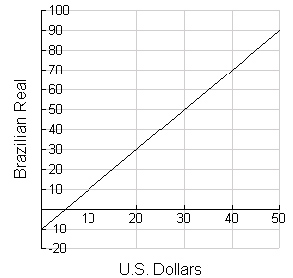
2. This graph shows the currency exchange that Scott received at
a local bank on his trip to Brazil in spring of 2007.
a. What is the slope of the line ?
b. What does the slope mean in this context?
c. Did the bank charge a fee for exchanging Scott’s
money? If so, how much? How do you know?
d. Find an equation that models this situation. Clearly
define your variables.
e. Scott sets up the proportion show below to figure out
how many Real he will get if he exchanges $50. Show
that the proportion does not give the right answer. Then explain WHY it
doesn’t work.
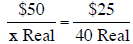
Intermediate Algebra
1. Recall the problem on Thomas Malthus, the British economist and clergyman who
hypothesized that as
the British population exceeded the food supply, mass starvation would occur.
The table below is based on Malthus’ calculations with years from 1800.
| Year |
 |
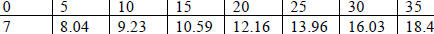| Population of England in millions |
a. According to Malthus’ calculations, how long does it
take the population of England to double?
Based on your answer, write an algebraic model using fractional exponents for
the population of
England. Define the variables.
b. By what percent does the population of England grow every 5 years? Based on
your answer,
write another algebraic model using fractional exponents for the population of
England. Define
the variables.
c. Find a regression model for this data. Define your variables. What is the
yearly percent growth in
your regression model?
d. Use what you have learned today to reconcile these models. In other words,
explain why these
models are equivalent or not equivalent.
2. You are the head of the marketing division of a large company. Marketing
research has shown that the
company’s annual profit, P in thousands of dollars, is related to the amount
spent on advertising, x in
hundreds of thousands of dollars, by the quadratic function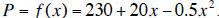 
The CEO of
the company is willing to spend up to four million dollars on advertising this
year. What advice do you have
for the CEO? This CEO likes very precise information. He always wants very
succinct advice, but he is also
interested in the “whole picture”. While he may not be interested in the details
of your analysis, he insists
on full documentation in case he later wants to review the facts. Write a report
that gives clear advice for
the CEO and fits the above specifications.
