5 Addition
Addition of p -adic numbers is similar to the addition of p-ary numbers. However,
we add the digits
and propagate the carries from left to right. As an example, we compute 2/3+5/6
= 3/2 for p = 5.
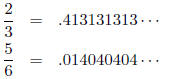
The addition operation proceeds as follows:
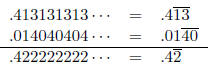
As a check, we convert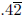 
to rational
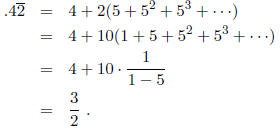
6 Subtraction
We complement the subtrahend and add it to the minuend, i.e., α − β = α + (−β).
Let α = 2/3
and β = 5/6, then
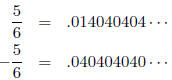
Thus, we compute 2/3 − 5/6 = −1/6 as
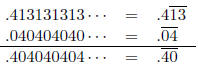
Now, we convert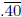 
to
rational using
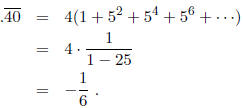
7 Multiplication
A p-adic number is called unit if it is not a multiple of a negative power of p
and its first digit is
nonzero. For example,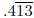 
and
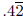are units while
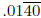and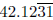 
are
not. A non-unit p-adic
number α can always be written in the form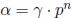 
where γ is a unit. For example,
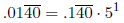
and
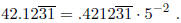
Let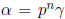 
and
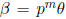, then 
.
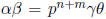We can thus restrict multiplication of any two
p-adic numbers to multiplication of units. The multiplication can then be
carried similar to the
case of p-ary numbers. To multiply 2/3 and 5/6, we get the Hensel codes‘
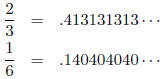
The multiplication operation is illustrated below:
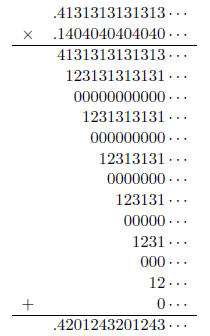
Thus, the result is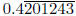 
which is equal to
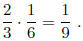
8 Division
Again, we will only consider the division of p -adic units. Consider the
following p-adic units:
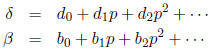
with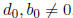 
. The quotient α
= δ/β can be written
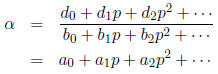
where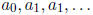 
are the digits
of α. Since δ = β · α, we have
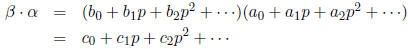
Even though the p-adic digits
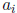and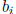 
lie
in the interval [0, p − 1], we cannot assume that the
integers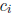 
lie in this interval. Hence we
write
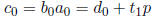
where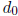 
∈ [0, p − 1].
Then 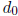is the first digit in the p-adic
expansion for βα and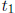 
is the carry
which must be added to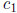 
. Thus,
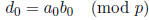
which implies
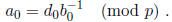
This turns out to be the rule for obtaining each digit of
the expansion for α. At each stage of
the standard long division procedure, we multiply
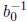(mod p) by the first digit of the partial
remainder and reduce the result modulo p.
As an example, we divide 2/3 by 1/12. We have
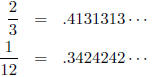
The first digit of the divisor is
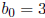and its multiplicative inverse modulo 5 is
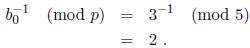
The first digit of the partial remainder (which, in the
first step , is the dividend) is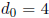 
, which
gives
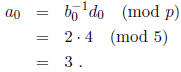
Thus, we obtain the first digit of the quotient. We then
update the partial remainder by subtracting
3 times the divisor from it.
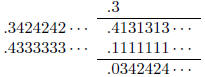
To obtain the second digit, we multiply
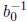(mod p) by the first
digit of the partial remainder
and reduce the result modulo p.
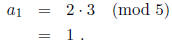
Thus, the second step of the division procedure gives us
This procedure produced the partial remainder which is
zero , hence we terminate the expansion.
In general, this will not happen and we will have to continue until the period
is exhibited. As a
check we observe that 2/3 ÷ 1/12 = 8 and 8 = .31 for p = 5.
We note that the division of p-adic numbers is deterministic and not subject to
trial and error
as is the case for division of p-ary numbers.
