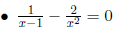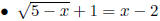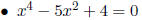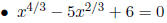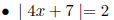1.4 Rational Expressions
A rational expression is a fractional expression where
both the numerator and denominator are polynomials.
1.4.1 Domain of an algebraic expression
Some things to look for are:
• The denominator can ’t be zero. If a value of x makes the denominator zero, we
must exclude it from
the domain.
• For even powered roots , whatever is under the radical must be ≥ 0.
Example: What is the domain of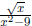 
?
1.4.2 Working with Rational Expressions
Working with rational expressions is just like working with fractions.
Examples
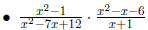
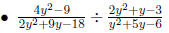
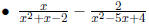
1.4.3 Compound Fractions
Compound fractions are fractions within fractions.
There are two ways of simplifying compound fractions.
• Method 1 is to work with the numerator and denominator separately.
• Method 2 is to find the LCD of all the fractions in the numerator and
denominator and to multiply
top and bottom by this LCD.
If there are negative exponents, write everything with positive exponents using
the rules of exponents.
Examples:
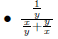
To simplify rational expressions with fractional
exponents, factor out the power of x with the smallest
exponent (if possible).
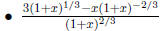
1.4.4 Rationalizing the Denominator or Numerator
If the numerator or denominator is of the form
,
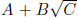we rationalize by multiplying top and bottom
by the conjugate. The conjugate normally requires just changing one sign
while leaving the other sign the
same. The conjugate of
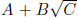is
.
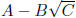Why? When you multiply these two expressions together
you get A2 − B2C, which has NO radicals.
Examples
• What are the conjugates of:
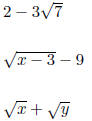
• Rationalize the denominator of
.
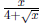• Rationalize the numerator of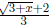 
.
1.5 Equations
1.5.1 Types of Equations
• Linear Equations can always be written in the form ax + b = 0.
To solve linear equations, use basic algebra, but remember what you do to one
side, you MUST do to
the other side.
• Quadratic Equations can be written in the form ax2 + bx + c = 0 with a
≠ 0.
1.5.2 Solving Quadratic Equations
The Zero- Product Property tells us if AB = 0, then either A = 0 or B = 0.
Example: Solve this equation by factoring. 2x2 − x = 3
Example: Solve (x − 5)2 = 17
What happens if your expression is not factorable or you can’t remember how to
factor it? Use THE
QUADRATIC FORMULA:
The roots (or solutions) of the quadratic equation ax2 + bx + c = 0 where a
≠
0, are:
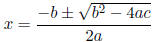
Example: Solve the equation x2 + 3x + 1 = 0
1.5.3 Completing the Square
To make x2 + bx a perfect square, add
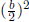. Although it is sometimes easier just to use the quadratic
formula, there are times when completing the square is necessary .
Example: Solve this equation by completing the square: 3x2 − 6x − 1 = 0
1.5.4 The Discriminant
The discriminant of a quadratic equation is D = b2 − 4ac. It is the part of the
quadratic formula that is
underneath the square root. The discriminant tells us how many real solutions
the equation has. There are
3 cases.
1. D>0.
2. D=0
3. D<0
Example: How many real solutions does 4x2 − 5x + 2 = 0 have?
An object thrown up at an initial speed of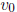 
ft/s will reach a height of h feet
after t seconds based on the
formula
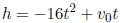
Suppose I throw a ball up with a speed of 48 ft/s.
a) When will the ball fall back down to me?
b) When will it reach a height of 32 ft.?
c) Will it reach a height of 64 ft.?
d) How high will the ball go?
1.5.5 Other types of equations
• Equations with Fractional Expressions. Multiply both sides by the LCD and then
solve.
• Equations with Radicals: Isolate the square root on one side of the equation
and then square both
sides. However, you must check for extraneous solutions.
• Equations of Fourth Degree of Quadratic Type: Let y = x2, and then solve a
quadratic equation in y.
After you have done this, solve y = x2 for x.
• Equations with Fractional Powers of Quadratic Type: Use some trial and error
to determine how to
transform the equation into a quadratic. Then check for extraneous solutions.
• Absolute Value Equations: Isolate the absolute value and treat cases.
Examples
