The exam covers Sections 2.6–2.9, 3.1–3.2, and 3.4–3.7. No calculators of any
kind will
be allowed. No formula sheets will be given on the exam, and none may be brought
into the
exam.
Formulas/definitions:
• The formula for a (tangent) line: y − yo = m(x − xo)
• The definition of the derivative:
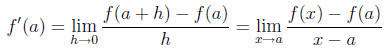
The first is better for high- order polynomials ; the second
is better for low -order polynomials,
fractions , roots, and such.
• Local minimum (maximum) at x = a: f decreasing
(increasing) for x slightly less than
a, f increasing (decreasing) for x slightly greater than a.
• Inflection point at x = a: f changes its concavity at x
= a.
• Simplifications:
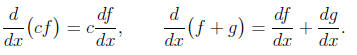
• The power rule :
• The product rule :
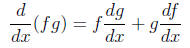
• The quotient rule:
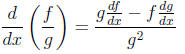
• The chain rule:
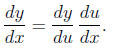
• Elementary functions:
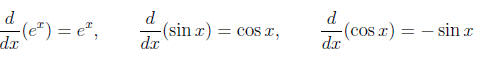
• Elementary inverse functions:
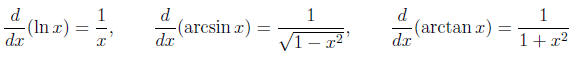
Standard tricks/techniques:
• For computing derivatives from the definition:
– factoring polynomials (if using x -> a); expanding polynomials (if using h ->
0)
– rationalizing differences of square roots: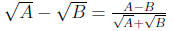
– subtracting fractions (get a common denominator
• For graphing f ' given f, or graphing f given f':
– f increasing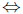 
f' > 0; f decreasing
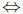f' < 0 (with few exceptions)
– f concave up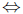 
f' increasing
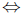f'' > 0;
f concave down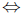 
f' decreasing
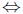f'' < 0;
• – To graph f' from f: first figure out when f' is
positive or negative (from direction
of f); then modify so f' is increasing/decreasing correctly (from concavity of
f).
– To graph f from f': first figure out when f is increasing or decreasing (from
sign
of f'); then modify so f is concave up/down correctly (from direction of f').
• To compute derivatives from rules. Rewrite all roots
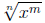as powers:
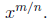Rewrite
all reciprocals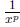 
as powers:
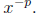
• To compute derivatives of any trigonometric functions ,
first write them all in terms of
sine and cosine, then use the product/quotient/chain rules.
• When combining rules (e.g. the product rule and the
chain rule), do simpler computations
on the side in a little box, so you can be more systematic about it. This way,
minor errors will be easy to detect. Avoid doing too much in your head.
• Implicit differentiation:
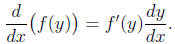
– e.g., if y = arcsin x then x = sin y and
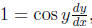, so you can use this instead of
remembering the formula for derivative of inverse trig functions.
– e.g.,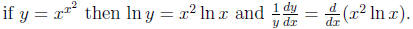 
– e.g., if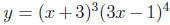 
then ln y = 3 ln (x + 3)+4 ln (3x
− 1), and you don’t
have to use the product rule.
S.F. no’s (never do these!):
• The idiot’s constant rule:
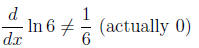
• The nitwit’s product rule:
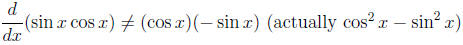
• The simpleton’s quotient rule:
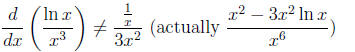
• The dunce’s chain rule:
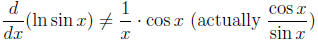
• The numskull’s chain rule:
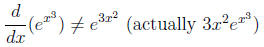
• The chucklehead’s power rule:
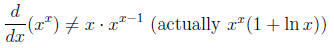
• The dupe’s derivative:
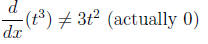
• The buffoon’s tangent line: tangent to x^2 at (2, 4) is
not y − 4 = 2x(x − 2) (actually
y = 4 = 4(x − 2))
• The schlemiel’s inflection point: if f(x) = x^4 then
f''(0) = 0, but 0 is not an inflection
point (actually f does not change concavity)
• The lamebrain’s local extremum: if
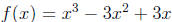then f'(1) = 0 but x = 1 is
not an extremum (actually it is a stationary point)
• The bungler’s direction rule: since f' is increasing, f
must be positive (actually it’s
the other way around)
• The oaf’s concavity principle: since f' is concave down,
f must be decreasing (actually
it’s the other way around)
Know the key counterexamples:
• when f'(a) does not exist
– f is not continuous at
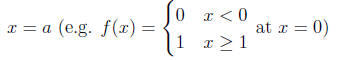
– f has vertical tangent line at x = a (e.g. f(x) =
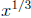at x = 0)
– f has different derivatives from the left and right
(e.g. f(x) = |x| at x = 0)
• stationary point: f'(a) = 0 but f' does not change sign
at x = a (e.g. f(x) = x^3 at
x = 0)
• {not an inflection point}: f''(a) = 0 but f'' does not
change sign at x = a (e.g.
f(x) = x^4 at x = 0)
• f' positive implies f increasing, but f may be
increasing without f' always being
positive (e.g. f(x) = x^3)
Tools for memory:
• d/dx (sin x) = cos x and d/dx (cos x) = −sin x. Remember
the sign using graphs of sine and
cosine.
• Quotient rule: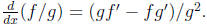 
Remember the sign by knowing special case
g = 1 (get f' either way).
• Every derivative-from-the-definition is a limit of the
form 0/0 and involves cancelling out
an h or an (x − a) from top and bottom. If you don’t get this, your algebra is
wrong.
• Chain rule:
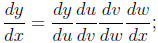
the differentials should cancel in pairs.
• If you’re ever not sure whether a rule is valid, check
it on simple nonconstant functions
(like powers of x) that you can also compute another way.
Review problems:
Make sure you know exactly how to do all of these. It’s not enough to skim
through the
list! If you haven’t tried all of these problems, and you do badly on the exam,
it’s your own
fault.
If you get stuck with any of them, go back and do some extra exercises from the
corresponding
section until you understand.
• Chapter 2 review, pp. 175–178: (Concept check): 14–16;
(True-false): 15–17; (Exercises):
25b, 26b, 27, 28ab, 30, 32–34, 35ab, 36c, 37–38, 40, 41–43, 46.
• Chapter 3 review, pp. 255–257: (Concept check): 1, 2, 3cd, 4; (True-false):
1–12 (very
important!); (Exercises): 1–13, 16–28, 31–34, 35–42, 43ab, 44a, 47–62, 64abe,
65–66,
68, 70, 73.
