On Wednesday we discussed finding the vertex of a
parabola . If we have a quadratic in
the form y = a(x – h)2 + k, then the vertex is at the point (h,k), indeed the
reason for
writing the function in the form is exactly that it lets us spot where the
vertex is easily.
Now the vertex is interesting because it is the lowest (or highest) point on the
parabola .
But sometimes we are interested in when a quadratic function takes some
particular
value. In this studio, we will look at how to find when a quadratic function
takes the
value 0. Once we have developed efficient ways to find when the function takes a
0
value, it will be reasonably easy to work out when it takes any other set value
we are
interested in.
Go to the class web site and download the file slidingparabola. xls. When you
open the
spreadsheet, be sure to choose “Enable Macros” if you are asked. This file shows
the
graph of the parabola y = a(x – h)2 + k on a fixed window, [-10, 10] x [-10,
10]. The
coefficients a , h, and k, are adjusted by moving three sliders at the top of the
page. The
specific values of a, h, and k are listed to the left of the sliders. The zeros
of the function ,
that is the x values where the function takes the value 0, or, in geometric
terms, the places
where the graph crosses the x-axis, are given below the
1. Move the sliders around. Write a short paragraph describing how changing the
values of each coefficient changes the graph of the function.
2. Now move the sliders to set the value of a = 1 and h = 0. Just move the
slider for k
around. What value of k gives you the following pairs of zeros?
a. -1 and 1
b. -2 and 2
c. -3 and 3
3. Now move the sliders for h and k (while a is still 1). Record which values of
h and k
give you the following zeros.
a. 3 and 5
b. -2 and 1
c. 4 and 4 (a double root )
4. Using the data you’ve gathered above, can you find a pattern for where the
zeros of
(x – h)2 + k will be? Write down the pattern. Justify your pattern by using
algebraic
manipulations to solve (x – h)2 + k = 0.
5. You may have noticed when you moved the sliders around that sometimes the
zeros
were listed as #NUM! This means that there were no zeros, because the parabola
never crossed the x-axis. For what values of h and k are there no zeros? For
what
values of h and k is there a double root ( two equal zeros)?
Now that we’ve worked out the easier monic case (with a =
1), we’re ready to tackle the
full situation where we can have a take other values.
6. Move the slider for a to set a = 0.5. Repeat your work from problems 2 and 3
and
record the new values for k or for h and k that give the requested zeros.
7. Now move the slider for a to set a = 3. Repeat your work from problems 2 and
3 and
record the new values for k or for h and k that give the requested zeros.
8. Now move the slider for a to set a = -2. Repeat your work from problems 2 and
3 and
record the new values for k or for h and k that give the requested zeros.
9. Using the data you’ve gathered above, can you find a pattern for where the
zeros of
a(x – h)2 + k will be? Write down the pattern. Justify your pattern by using
algebraic
manipulations to solve a (x – h)2 + k = 0.
10. For what values of a, h, and k are there no zeros? For what values of a, h,
and k is
there a double root (two equal zeros)?
Note that now that we have a formula for finding the zeros (roots) of a
quadratic equation
of the form a(x – h)2 + k = 0, we can build a formula for finding the roots of a
quadratic
equation of the form ax2 + bx + c = 0. We just need to use our rules for
completing the
square to convert this into the a (x – h)2 + k = 0 form, and then apply the
formula we have
for that form (careful, the a has different meanings in the two different
forms). You can
find the details worked out in section 2.2 of the text (pp. 172-173). The
resulting formula
you get is that the zeros of ax2 + bx + c = 0 are given by the quadratic
formula,
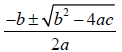
Note the ± sign , indicating that there are two roots, one corresponding to the +
and one
corresponding to the –. Finally, suppose we want to solve for a value other than
0. For
example, suppose we want to solve
x2 + 4x + 2 = 14.
We can convert this into solving for a zero value instead of solving for 14 by
subtracting
14 from both sides to get
x2 + 4x – 12 = 0.
Now we can solve this by any of our techniques. We can factor it as (x + 6)(x –
2)=0,
apply the quadratic formula, or complete the square and apply our simpler
formula for
that case. In any event, we find x = -6 and x = 2 are the two solutions. Note
that we will
usually get two solutions to a quadratic equation, but that we can also have no
solutions
and will occasionally have a double root, where our two solutions turn out to be
the same
number. We’ll discuss later why it is still useful to think of these as two
solutions, even
though they are the same.



