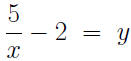Simplifying Algebraic Expressions

constant- represents a quantity that does not change.

examples: 3, 4.8,π

variable- symbol representing a quantity that does

change examples: x, y, a

coefficient- a multiplier

examples:

4x, 4 multiplies x , so 4 is the coefficient of x

3xyz- the coefficient of z is 3xy

algebraic expressions - any combination of constants,

variables and operation symbols

examples: 2x + 45 and

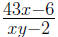
algebraic terms parts of an algebraic expression

separated by + or −

examples: 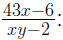43x is a term, as is xy

How many terms are in the expression ?

Equation- statement that two algebraic expressions

are equal

Example: 5x² − 3x = xy

Simplifying Algebraic Expressions

Order of Operations :

Parenthesis
Exponents
Multiplication and Division
Addition and Subtraction

(Please Excuse My Dear Aunt Sally)

Example: Simplify

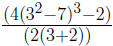
Multiplying Algebraic Expressions

For any real numbers a , b, c and d:

a(b + c) = ab + ac
(a + b)(c + d) = ac + ad + bc + bd
note: (a + b)² = (a + b)(a + b) = a² + 2ab + b²

“Expand” means “multiply out”

Expand the expression : (x + 4)(x − 2)

Independent Variable- the “input” variable, usually,

but not always, x

Dependent Variable- the “output” variable, depends

on the input, usually, but not always, y

Linear Function - a relation between the independent

and dependent variables characterized by a common

difference or slope

Two important parameters:

start value, or seed (often P₀or b)

common difference , or slope (often d or m)

Slope- describes direction and steepness of a line

Positive slope - line increases from left to right

Negative slope- line decreases from left to right

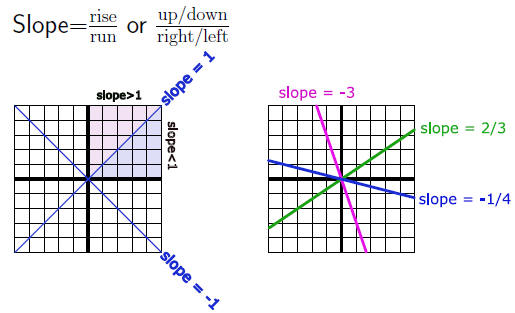
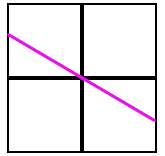
Estimate the slope:

Graphing lines using intercepts

x-intercept- function value when y = 0

y-intercept- function value when x = 0

Name intercepts:

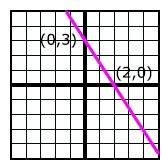
Graph:x-intercept: -3,
y-intercept: -1.

Graphing with slope and y -intercept

Plot the y-intercept.
Use slope 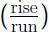to plot another point.

Connect the points, extending the line both

directions.

Example:

Graph a line with y-intercept 1 and slope 3/2:

Direct and Indirect Variation

Direct Variation- two variables both increase

proportionally

Indirect Variation-one variable increases, the other

decreases

variation constant- usually k, also called constant of

proportionality

Direct variation is modeled by: y = kx

We say: “y varies directly with x” or “y is directly

proportional to x”

Examples:

• profit and cost of an item

• The distance a spring stretches varies directly as

the amount of weight that is handing on it.

Example: A weight of 50 pounds stretches the spring

10 inches. How much would the spring be stretched

with a weight of 60 pounds?

direct variation, so use y = kx

Let y by the distance, and x be the weight.

10 = k · 50 or k = 1/5

Model: y = (1/5)x

y = (1/5) · 60 = 12

A 60 pound weight will stretch the spring 12 inches.

Indirect variation modeled by: y = k/x

We say “y varies indirectly with x” or “y is indirectly

proportional to x”

Examples:

• time in dorms and appeal of dorm food

• wing beats and wing length

Example: Herring gull- 24 centimeter long wings

beat 3 times per second

assume variation constant remains the same

How fast will 12 centimeter wings beat?

Let y represent the wing beats and x represent the

length of the wing.

Indirect variation, so use y = k/x

3 = k/24 or 3(24) = k = 72

Model: y = 72/x

y = 72/12 = 6

A bird with wing length 12 centimeters will beat 6

times per second.

Solving Literal Equations

Consider

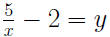
y is determined by the value assigned to x. Call x the

independent variable, and y the dependent variable.

Change the roles of dependent and independent by

solving for x:

(remember that the equation must balance, what

happens on one side must happen on the other also)