Here are some thoughts I was having while considering what
to put on the second midterm.
The core of your studying should be the assigned homework problems: make sure
you really
understand those well before moving on to other things ( like the old midterms on
the test
archive).
• Chapter 7 - Quadratic Modeling
– The quadratic function is introduced. You should know the significance of the
vertex
and how to find it. You should be able to sketch the graph of a given quadratic
function.
– You should be able to determine the maximum and minimum value of a quadratic
function on a specified interval.
– You should be able find the maximum or minimum possible value of a quantity by
expressing it as a quadratic function of some other quantity (e.g., area of a
rectangular
enclosure as a function of the width of the enclosure, etc.). Problem 7.10-7.14
all
involve this idea.
• Chapter 8 - Composition
– In addition to combining two functions into a new function via arithmetic (the
way
we can combine two numbers into a new number), we can also combine two functions
via composition.
– You should understand what f(g(x)) means, and how to express a rule for f (g(x))
given rules for f(x) and g(x).
– I especially like problems 8.3, 8.4, 8.5.
• Chapter 9 - Three Construction Tools
– You should understand horizontal and vertical shifting, and horizontal
and vertical
scaling (aka dilating)
– You should understand how to derive the graph of g(x) = af(bx + c) + d from
the
graph of f(x) (see, e.g., problem 9.2)
– I especially like problems 9.2, 9.3, 9.4, and 9.7
• Chapter 11 - Inverse Functions
– Another very short chapter.
– You should understand what an inverse function is, what conditions a
function
must satisfy in order to have an inverse (do all functions have inverses? can
you tell
if a function has an inverse by looking at its graph?), and how to find the
inverse of
a given function
You should understand what a one-to-one function
is, and what is special about the
graph of a one-to-one function
– Problems 11.2, 11.6, and 11.8 are particularly good.
• Chapter 12 - Rational Functions
– An important chapter, it introduced a new class of functions for modeling.
– You should be able to find the asymptotes (horizontal and vertical) of
a linear-to-linear
rational function, and be able to sketch the graph of a rational function
like
those in problem 12.1(a) or (b).
– You should be able to model with linear-to- linear rational functions.
This comes
down to finding a rational function of the form
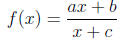
whose graph
1. passes through three given points
or
2. has a given asymptote and passes through two given points
or
3. has two given asymptotes and passes throuh one given point
You will need to translate the language of the modeling problem. Take a look at
old
midterm 2 exams from the archive for examples to work on.
Pay particularly close attention to the words “linear-to-linear”.
Note that a linear-to- linear function is not a linear function.
– I especially like problems 12.6, 12.7, 12.8, 12.10, and 12.11.
• Chapter 13 - Measuring an Angle
– You should understand how to convert between degrees and radians
– You should understand and be able to use the relationships between radii,
angle,
arc length and area
– I like problems 13.8 and 13.9 (check the electronic version of the text at the
120 Materials
Website if your copy of the text doesn’t show the shading well).
• Chapter 14 - Measuring Circular Motion
– You should understand the various measures of angular speed (aka
angular velocity),
like rpm, radians per second, or degrees per hour
– You should understand the relationship between
radius, angular speed and linear
speed
– You should know how to solve a belt -and-pulley problem (e.g., the bicycle
example
from lecture, example 14.4.1, problems 14.8, 14.9 and 14.11)
– I also like problems 14.5 and 14.7.
• Chapter 15 - The Circular Functions
– This chapter introduces the trigonometric functions .
– You should be able to solve problems using the idea of trigonometric functions
as
ratios of sides of right triangles (e.g., problems 15.4, 15.7, 15.8) and some
algebra
– You should understand the definitions of sin x and cos x using the unit
circle ; you
should be able to determine certain simple properties of the functions sin x and
cos x
from this definition (e.g., the range, the domain, the graph, the values at
certain
value of x, like x = 5π /2)
– You should be able to determine the location of an object moving circularly
given information
about its speed and starting location (e.g., problems 15.2, 15.5, 15.9, 15.15,
and the three non-textbook Chapter 15 problems)
• Chapter 16 - Trigonometric Functions
– This is a short chapter which adds some final touches to our knowledge of the
functions
sin x and cos x and related functions.
– I like problems 16.3 and 16.4.
• Chapters 17 - Sinusoidal Functions
– You should understand the notion of a sinusoidal function as a
shifted/stretch/squished
version of the function sin x.
– You should understand the effect of the four parameters A,B,C and D on the
graph
of
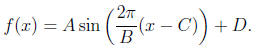
– You should be able to model with sinusoidal functions.
In particular, you should
be able to determine the parameters A,B,C, and D from a verbal description of a
quantity that varies sinusoidally with time (see problems 17.2, 17.3, 17.4,17.6)



