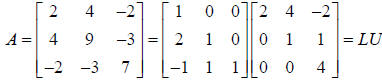Covered in class: 4, 6, 7
1. When doing integer calculations one can many times proceed exactly, except of
course in certain situations, e.g. division 5/2=2.5. However, when doing
floating point
calculations rounding errors are the norm, e.g. 1./3.=.3333333… cannot be
expressed
on the computer. Thus the computer commits rounding errors to express numbers
with machine precision, e.g. 1./3.=.3333333. Machine precision is 10-7 for
single
precision and 10-16 for double precision. Rounding errors are only one source of
approximation error when considering floating point calculations. Some others
are
listed below.
2. Approximation errors come in many forms:
a. empirical constants – Some numbers are unknown and measured in a
laboratory only to limited precision. Others may be known more accurately
but limited precision hinders the ability to express these numbers on a finite
precision computer. Examples include Avogadro’s number, the speed of light
in a vacuum, the charge on an electron, Planck’s constant, Boltzmann’s
constant, pi, etc. Note that the speed of light is 299792458 m/s exactly, so we
are ok for double precision but not single precision.
b. modeling errors – Parts of the problem under consideration may simply
be
ignored. For example, when simulating solids or fluids, sometimes frictional
or viscous effects respectively are not included.
c. truncation errors – These are also sometimes called discretization
errors and
occur in the mathematical approximation of an equation as opposed to the
mathematical approximation of the physics (i.e. as in modeling errors). We
will see later that one cannot take a derivative or integral exactly on the
computer so we approximate these with some formula (recall Simpson’ s rule
from your Calculus class).
d. inaccurate inputs – Many times we are only concerned with part of a
calculation and we receive a set of input numbers and produce a set of output
numbers. It is important to realize that the inputs may have been previously
subjected to any of the errors listed above and thus may already have limited
accuracy. This can have implications for algorithms as well, e.g. if the inputs
are only accurate to 4 decimal places, it makes little sense to carry out the
algorithm to an accuracy of 8 decimal places. This issue commonly resurfaces
in scientific visualization or physical simulation where experimental engineers
can be unhappy with visualization algorithms that are “lossy”, meanwhile
forgetting that the part that is lost may contain no useful, or accurate
information whatsoever.
3. More about errors
a. In dealing with errors we will refer to both the absolute error and the
relative
error.
i. Absolute error = approximate value – true value
ii. Relative error = absolute error / true value
b. One needs to be careful with big and small numbers, especially when dividing
by the latter. Many times calculations are non-dimensionalized or normalized
in order to operate in a reasonable range of values. For example, consider the
matrix equation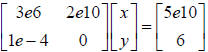 
. Recall that these are just
two
algebraic equations.
i. We can divide the first equation by 1e10, this is called row scaling, to
obtain: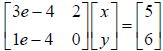 
.
ii. Similarly, we can define a new variable z =(1e-4)x, this is called
column scaling, to obtain: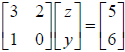 
. This final equation is
much easier to deal with than the original. It can be solved for z and y,
and x can then subsequently be found from z.
4. Condition Number. A problem is ill-conditioned
if small changes in the input data
lead to large changes in the output. By convention of definition, large
condition
numbers are bad (sensitive), and small condition numbers are good (insensitive).
If
the relative changes in the input and the output are identical, the condition
number
will be unity.
5. Stability and Accuracy. For well-conditioned problems, one can attempt
to solve
them on the computer, and then the terms stability and accuracy come into play.
Stability refers to whether or not the algorithm can complete itself in any
meaningful
way, i.e. unstable algorithms tend to give wildly varying, explosive data that
usually
lead to NaN’s. On the other hand, stability alone does not indicate that the
problem
has been solved. One also needs to be concerned with the size of the error,
which
might still be enormous, e.g. no significant digits correct. Accuracy refers to
how
close we are to the true solution for stable algorithms.
6. Do I need to worry about all this stuff? An example… Consider the quadratic
equation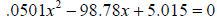 
with solutions x=1971.605916
and
x=.05077069387 to 10 digits of accuracy . Recall the quadratic formula
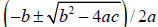where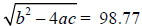 
to 4 digits of accuracy. Then our
solutions are (98.78+98.77)/.1002=1972 and (98.78-98.77)/.1002=.0998, and the
first
root is correct to 4 decimal places while the second root has zero decimal
places of
accuracy. An alternative quadratic formula can be obtained by multiplying the
top
and bottom by 
to de-rationalize the
quadratic formula to
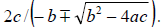Using this
formula we obtain 10.03/(98.78-98.77)=1003 and
10.03/(98.78+98.77)=.05077 as our two roots. Now the second root is correct to
four
decimal places while the first root is highly inaccurate. So the remedy here is
to use
the usual formula for the first root and the de-rationalized formula for the
second root.
And the lesson is, did you know this was an issue? How would you like to debug a
piece of code with the correct quadratic formula and zero digits of accuracy for
a test
case?
7. So, what’s going on here? Well, the basic problem is that the specific
sequence of
operations performed in solving the quadratic formula above results in a large
error.
“ Subtractions followed by divisions cause errors.” Subtraction reveals the error
that
round-off makes. Division can amplify the round-off error. It is important to
understand that the operations themselves are not dangerous, but the specific
order
[aka the algorithm] can be, if not done correctly.
8. Another simple example of a common numerical pitfall is in the computation of
the
norm, or length, of a vector
.The naive way of
implementing this
algorithm { for (1,n) sum+=x(i)*x(i); return sqrt(sum); } can quickly overflow
the
MAX_FLOAT or MAX_DOUBLE on the computer (for large n). A safer algorithm
would be to let y=max(abs(x(i))) and then { for (1,n) sum+=sqr(x(i)/y); return
y*sqrt(sum); }.
Systems of LinearEquations
Covered in class: 1(a,d), 2, 3, 4, 5, 6
1. Systems of linear equations .
a. Given a system of equations: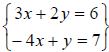 
, we can
write it in matrix form
as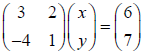
which we will commonly refer to as Ax=b.
b. Given A and b our goal is to determine x. The system of linear equations
Ax=b has a unique solution, no solution, or infinite solutions, as
you have
learned in your basic algebra class. Ideally, a piece of software would
determine whether there was a unique solution, no solution, or infinite
solutions. Moreover, in the last case, it should list the parameterized family
of
solutions. Unfortunately this turns out to be fairly harder than one would first
think.
c. Let’s start out by considering only square n · n matrices to get some
of the
basic concepts down. Later we’ll move on to more general rectangular
matrices.
d. One of the basic issues that has to be confronted is the concept of “zero”.
When dealing with large numbers, for example on the order of Avogadro’s
number, i.e. 1e23, zero can be quite large. In this case, for double precision
arithmetic, numbers on the order of 1e7 may be “zero”, i.e. 1e23-1e7=1e23.
On the other hand, when dealing with small numbers, such as 1e-23, then zero
will be much smaller. In this case, on the order of 1e-39. Difficulties with
finite precision arithmetic usually force us to non-dimensionalize or
normalize our equations. For example, consider the matrix equation
.
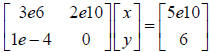
i. We can divide the first equation by 1e10, this is called row scaling,
to obtain: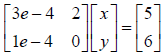
ii. Similarly, we can define a new variable z=(1e-4)x to obtain:
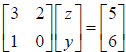. This is called column scaling. It
essentially
divides the first column by 1e-4.
iii. The final equation is much easier to treat with finite precision
arithmetic than the original one. It can be solved for z and y, and
then subsequently x can be determined from the value of z using
x=(1e4)z.
e. We say that a matrix A is singular if it is not invertible, i.e. if A
does not have
an inverse. There are a few ways of expressing this fact, for example by
showing that the determinant of A is identically zero, det(A)=0, or showing
that there is a nonempty null space, i.e. showing that Az=0 for some vector
z ≠ 0 .
i. The rank of a matrix is the maximum number of linearly
independent rows or columns that it contains. For singular matrices
rank < n.
ii. Singular matrices are the ones that have either no solution or an
infinite number of solutions.
f. We say that a matrix A is nonsingular if its inverse
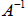exists. Recall that
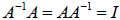, and thus Ax=b can be transformed into
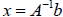where x is
the unique solution to the problem. Note that we usually do not compute the
inverse, but instead have a solution algorithm that exploits the existence of
the
inverse.
2. A diagonal matrix only has nonzero elements on the diagonal. For
example, consider
the matrix equation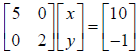 
where A is a diagonal
matrix. These equations
are easy to solve using division, i.e. the first equation is 5x=10 with x=2 and
the
second equation is 2y=-1 with y=-.5. For diagonal matrices the equations are
essentially decoupled.
a. Note that a 0 on the diagonal indicates a singular system, since that
equation
has either zero or infinite solutions depending on the b matrix, i.e. 0y=1 has
no solution and 0y=0 has infinite solutions.
b. The determinant of a diagonal matrix is obtained by
multiplying all the
diagonal elements together. Thus, a 0 on the diagonal implies a zero
determinant and a singular matrix.
3. An upper triangular matrix may have a nonzero diagonal and may be nonzero
above
the diagonal, but is always identically zero below the diagonal. It is
nonsingular if all
of the diagonal elements are nonzero. This guarantees a nonzero determinant,
since
the determinant is just the diagonal elements multiplied together, just as it is
for a
diagonal matrix.
a. An upper triangular matrix can be solved by back substitution.
Consider
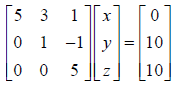where A is an upper triangular matrix. We start at the
bottom with 5z=10 and solve to obtain z=2. Then we move up the matrix one
row at a time. The next equation is y-z=10, or y-2=10 or y=12. Proceeding up
to the next row, we have 5x+3y+z=0 or 5x+36+2=0 or x=-38/5=-7.6. If the
matrix were bigger we would continue to proceed upward solving for each
new variable using the fact that all the other variables are known at each step.
4. A lower triangular matrix may have a nonzero diagonal and may be
nonzero below
the diagonal, but is always identically zero above the diagonal. It is
nonsingular if all
of the diagonal elements are nonzero. The linear system
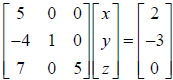has a
lower triangular A matrix. Lower triangular systems are solved by forward
substitution, which is the same as back substitution except that we start at
the top
with the first equation, i.e. 5x=2 or x=.4, and then proceed downward.
5. More general matrices usually require significantly more effort to construct
a
solution. For example, one might need to use Gaussian Elimination.
a. Define the basis functions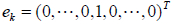 
where the 1 is
in the kth
row and the length of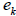 
is n.
b. In order to perform Gaussian elimination on a column of a matrix given
by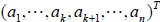 
, we define the size n· n elimination
matrix as
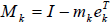where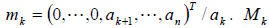 
adds multiples of
row k to the rows > k in order to create 0’s.
and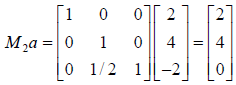 
c. The inverse of an elimination matrix is defined as
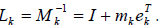
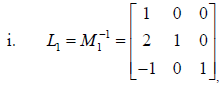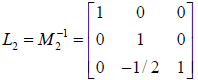
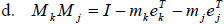and
and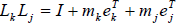 
for j > k, but not for
j < k
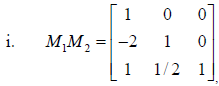and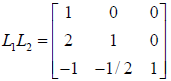 
6. LU factorization. If we can factorize A=LU where L is lower triangular
and U is
upper triangular then Ax=b is easy to solve since we can write LUx=b. Define z=Ux,
so that LUx=b can be rewritten as Lz=b and solved with forward substitution to
find
z. Now, knowing z, use back substitution on Ux=z to find x. Below we give an
example algorithm to solve: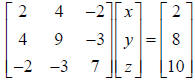 
.
a. First, we eliminate the lower triangular portion of A one column at a time
using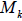 
in order to get
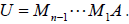Note that we also carry out the
operations on b to get a new system of equations
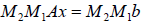or
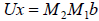which can then be solved for via back
substitution.
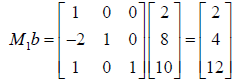
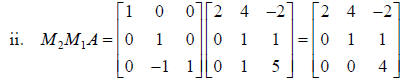and
and
iii. Finally solve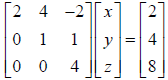 
via back substitution.
iv. Note that using the fact that the L matrices are the
inverses of the M
matrices allows us to writ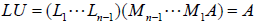e 
where
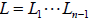can be formed trivially from the
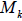to
obtain
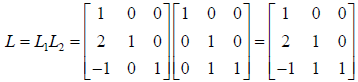. And thus, although
we never needed it to solve the equations, the LU factorization of A is :
