3. Determinant of a square matrix
[READ Ch. 4 on the book, for an introduction to the determinant]
We just summarize some properties of the determinant (see ยง 4.2).
Proposition 7. Let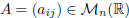 
. We have:
i) if A is a diagonal matrix,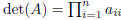 
. In
particular, det(In) = 1;
ii) if A has a zero row or column, then det(A) = 0;
iii)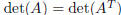 
;
iv) let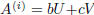 
, where b, c ∈ R and
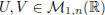. Let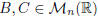 
,
the matrices obtained from A, substituting
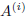with (respectively) U
and
V ; we have:
det(A) = b det(B) + c det(C)
[ an analogous result holds for the columns of A];
v) Let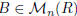 
be the matrix
obtained from A, by interchanging two rows
or columns; then det(B) = −det(A);
vi) If A has two proportional rows or columns, then det(A) = 0;
vii) (Binet's Theorem):
det(AB) = det(A) det(B) ;
viii) For all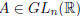 
, then:
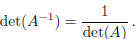
In particular, it follows that if
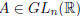, then det(A) ≠ 0.
Finally, we want to illustrate another important property
of the determinant (Laplace's
theorem). Some preliminary Definitions are necessary.
Definition. Let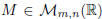 
and p, q positive
integers , such that 1 ≤p ≤m
and 1 ≤q ≤n. Let us choose p integers
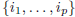such that
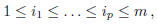
and q integers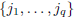 
such
that
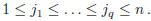
We define the submatrix of M relatively to the rows
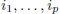and the columns
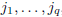, as the matrix obtained intersecting the
rows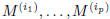 
and the
columns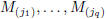 
.
This submatrix will be denoted by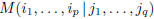 
.
One can verify that the submatrices of M, of type (p, q) are exactly:
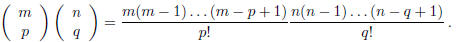
Definition. Let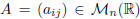 
,
with n ≥2. We call cofactor of aij , the
element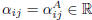 
, defined as:
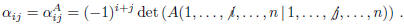
The matrix formed by all cofactors is called cofactor
matrix (or adjoint matrix) of
A and it is denoted by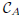 
:
Theorem 1 (Laplace's Theorem). Let
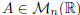, with n ≥2. For any
i, j = 1, . . . , n:
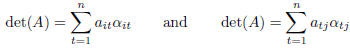
(these expressions are called , respectively, expansion of
the determinant with respect
to the row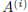 
and expansion of the determinant
with respect to the column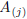 
).
Remark. This theorem provides a very useful tool for computing the
determinant
of a matrix. In fact, given a square matrix A of order n and fixed one of its
rows or columns, we can rewrite the determinant as the sum of n determinants of
submatrices of order n − 1; inductively, each of these determinants can be
written
as the sum of n − 1 determinants of submatrices of order n − 2 and so on ...
Obviously, the more zeros there are in the chosen row or column, the easier the
computation becomes.
Corollary 1. Let
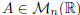. We have:
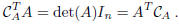
It follows that: if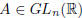 
,
then
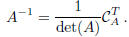
Proof. Let us start to verify that:
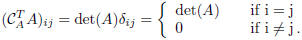
In fact,
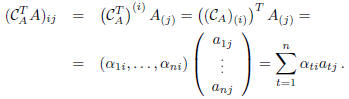
If i = j, the above sum is the expansion of the det(A)
with respect to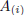 
; therefore,
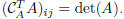
If i ≠ j, let us denote by B the matrix obtained from A, by substituting
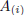with
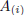. Let us compute the Laplace expansion of B
with respect to
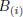. Observe
that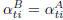 
(in fact, these cofactors do not
depend on the i-th row, and A and
B coincide apart from this row). Hence:
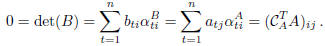
It remains to verify that:
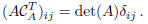
Proceeding as above, one can verify:
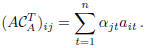
If i = j, the above sum is the expansion of the det(A),
with respect to 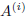; if i
≠ j,
let us denote by B the matrix obtained from A, by substituting
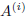with
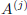. One
expands det (B) with respect to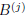 
and can
proceed as above.
