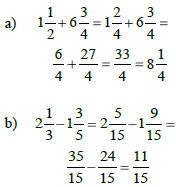Definitions
Fraction: a part of a whole.
Numerator: number of parts being considered.
Denominator: number of equal parts of the whole.
| Example: |
 numerator numerator |
 denomin ator denomin ator |
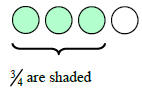
The graph of 3/4 on a number line:

Types of Fractions
Proper fraction: the numerator is less than the
denominator.
Example:3/4
Improper fraction: the numerator is greater than or
equal to the denominator.
Examples:6/6 and 9/5
Mixed Number: a whole number and a proper fraction.
Example: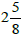 means
means
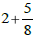
Division by 0 and 1
Zero divided by any number is 0. Division by 0 is
undefined.
Examples:0/9 = 0 and 7/0 =undefind
Any number divided by itself is 1:
Example:6/6 = 1 and x/x = 1
Writing Fractions and Mixed Numbers
The number 1 can be written as any fraction:
Example: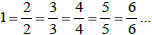
To write a whole number as a fraction, write the
whole number over 1:
Example:4 = 4/1
To write a mixed number as an improper fraction,
multiply the whole number by the denominator, add
the numerator, and keep the denominator:
Example: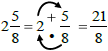
To write an improper fraction as a mixed number,
divide the numerator by the denominator. Use the
quotient to write the whole number. Place the
remainder in the numerator of the fraction, and keep
the denominator.
Example: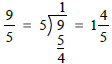
Divisibility Rules
Rule for 2: If a number ends in 0, 2, 4, 6, or 8 (even
number), divide by 2.
Rule for 3: If the sum of a number ‘s digits is a multiple
of 3, divide by 3.
Rule for 5: If a number ends in 0 or 5, divide by 5.
Rule for 10: If a number ends in 0, divide by 10.
Prime Factorization
A prime number can only be divided by itself and 1.
Primes: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 ...
To prime factor a number , divide the number by 2, 3,
5, 7 ... Then write the number as a product of its
prime factors.
Example:
60 = 2• 30
= 2• 2• 15
= 2• 2• 3• 5
= 22• 3• 5
Simplifying Fractions
A fraction is simplified when the numerator and
denominator have no common factors other than 1.
To simplify a fraction, factor the numerator and the
denominator. Cancel common factors and write a 1
in the numerator where necessary.
Example: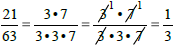
Example: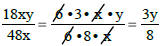
MULTIPLYING & DIVIDING FRACTIONS
Multiplying Fractions
1) Change mixed numbers to improper
fractions.
2) Multiply the numerators; multiply the
denominators.
3) Cancel common factors.
Examples:
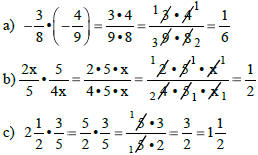
Dividing Fractions
1) Change mixed numbers to improper
fractions.
2) Think KFC:
Keep the first.
Flip the second.
Change the operation to multiplication .
3) Follow the rules for multiplying.
Examples:
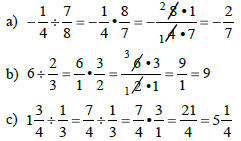
ADDING & SUBTRACTING LIKE
FRACTIONS
1) Add or subtract the numerators.
2) Keep the denominator.
3) Simplify the answer if necessary.
Examples:
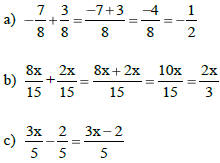
Adding & Subtracting Mixed Numbers
Like Denominators
1) Change mixed numbers to improper
fractions.
2) Add or subtract the numerators.
3) Simplify the answer.
Examples:
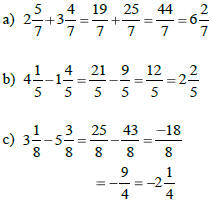
Finding the Least
Common Denominator (LCD)
List the multiples of the larger
denominator to find the LCD.
Example: Find the LCD of 5/6 and 3/8.
The LCD is 24 because 24 is the
smallest common multiple of 6 and 8.
Multiples of 8: 16, 24
Multiples of 6: 12, 18, 24
Writing Equivalent Fractions with
the LCD
To write an equivalent fraction with the
LCD, multiply the fraction by a form
of 1:
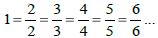
Example: Write each fraction with a
with a denominator of 24:
5/6 and 3/8
Multipl 5/6 by 4/4 because 6(4) = 24:
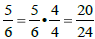
Multiply 3/8 by 3/3 because 8(3) = 24:
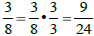
ADDING & SUBTRACTING UNLIKE
FRACTIONS
1) Find the LCD
2) Rewrite the fractions.
3) Add or subtract the numerators.
4) Simplify the answer.
Examples:
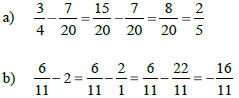
Adding & Subtracting Mixed Numbers
Unlike Denominators
1) Find the LCD and rewrite the
fraction parts.
2) Change mixed numbers to improper
fractions.
3) Add or subtract the numerators.
4) Simplify the answer.
Examples: