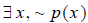This entire course requires you to write proper
mathematical proofs . All proofs should
be written elegantly in a formal mathematical style. Complete sentences of
explanation
are required. Do not simply write an equation; you must explain what the
equation is
giving and/or why it is being used. Moreover, all equations must be properly
aligned
with no scratch outs. Always give a conclusion.
We will begin by reviewing several standard methods of
proof using the following
basic definitions and using the facts that the sum and product of integers are
integers.
Divisibility: We say that a divides b if there exists an
integer k such that b = ka . For
example, 6 divides 18 because 18 = 3 × 6 , where k = 3 is an integer.
Even Number: An integer n is said to be even if it has the
form n = 2k for some integer
k . That is, n is even if and only if n divisible by 2.
Odd Number: An integer n is called odd if it has the form
n = 2 k +1 for some integer k .
Prime Number: A natural number n > 1 is said to be prime
if its only positive divisors are
1 and n . If n has other positive divisors , then n is called composite.
Rational Number : A real number x is called rational if x
can be written as a fraction
m / n , where m and n are integers with n ≠ 0. Otherwise, x is called
irrational.
Direct Proof
Consider the statements
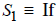p , then q , and
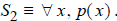At times we may try to
prove that these types of statements are true. To prove S1 directly, we assume
p is
true and then argue that q must also be true. To prove S2 is true, we pick an
arbitrary
x and argue that property p (x) must hold.
Example 1. Prove the following results directly:
(a) If n is an odd integer, then n2 +1 is even.
(b) If a divides b and b divides c , then a divides c .
(c) For all rational numbers x and y , the product x y is also a rational
number.
Proof. (a) Assume n is an odd integer. Then n = 2 k +1 for
some integer k . We then
have
n2 +1
= (2 k +1)2 + 1
= 4k2 + 4k + 2
= 2(2k 2 + 2k + 1)
= 2l ,
where l = 2k 2 + 2k + 1 is an integer because k is an
integer. Thus, n2 +1 has the form
of an even number, and so n2 +1 is even. QED
(b) Assume a divides b and b divides c . Then b = ka for
some integer k , and c = jb
for some other integer j . Thus,
c = jb = j (ka) = ( jk )a .
Because the product of integers jk is still an integer, we
have that a divides c . QED
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
- - - - - - - - - - - - - - - - - - - - - - - - - - -
(c) Let x and y be rational numbers . Then x = m / n and y
= j / k for some integers m ,
n , j , and k , with n ≠ 0 and k ≠ 0 . Then
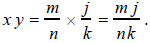
The products of integers m j and nk are still integers,
and nk cannot be 0 because
neither n nor k is 0. Thus, x y is in the form of a rational number and
therefore x y is
rational. QED
Indirect Proofs
Given an implication
,
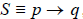its contrapositive is ~ q → ~ p , which is logically
equivalent to the original implication. In order to prove that S is true, it
might be easier
to prove that the contrapositive is true. That is, we can assume that q is not
true, and
then argue that p is not true.
Another common method used to prove p → q is a proof by
contradiction. In this
case, we assume that p is true but that q is not true. We then argue that a
mathematical
contradiction occurs. We conclude that q in fact must be true.
Proof by Contrapositive
To prove p → q,
assume that q is not true,
then argue that p is not true.
Proof by Contradiction
To prove p → q,
assume that p is true but q is not true.
Then argue that a mathematical
contradiction occurs.
Notes: (i) A logical statement is often a conjunction a
∧ b (a and b ) or a disjunction
a ∨ b (a or b ). We apply DeMorgan’s Laws to obtain
the negations of these statements
as follows:
(ii) The negation of “one or the other but not both” is
given by “both or neither”.
(iii) A logical statement may be in terms of a quantifier
such as “for every x , property
p(x ) holds.” The negation is “there exists an x for which p(x ) does not hold.”
Statement:
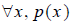Negation:
