Maxima and Minima for Multivariable Functions

Recall how we determine maxima and minima for single- variable functions : for some function
f(x), we look for critical points 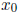(i.e. points for which f'(x) = 0) and at such a point, we consider
f''(x):

We now want to extend this work to multivariable functions.

Iterated Partial Derivatives
Now the first task is to generalize the notion of higher- order derivatives from single-variable
calculus. To do this, we naturally want to differentiate the partial derivatives of our function. For
example, consider f : R² → R¹ which is C¹ (i.e. its partial derivatives exist and are continuous).
We can consider each partial of f and differentiate it to get

We call such derivatives iterated partial derivatives, while 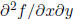and 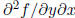are called
mixed partial derivatives. An important fact is that if f : Rⁿ → R^m is C², then the mixed
partial derivatives of f are equal. That is

This is an important result, and we will be using it often. You should definitely commit it (and its
conditions) to memory.

Exercise: Compute all second-order partial derivatives for 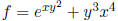(do not assume the
mixed partials are equal).

Taylor’s Theorem
Let us remind ourselves of the statement of Taylor’s theorem from single-variable calculus:

We will not delve into the proof of Taylor’s theorem for the single-variable or the multivariable
case. But let us state the theorem in the general case:

For the sake of exposition, let us state what happens when we take first and second-order derivatives:

In the case of single-variable functions, we can expand our function f(x) in an infinite power
series, which we call the Taylor series:

provided you can show that 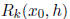→ 0 as k → 0. We can do the same for multivariable
functions by replacing the preceding terms by the corresponding ones involving partial derivatives
provided we can show 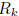→ 0 as k → 0.

Exercise: Compute the second-order Taylor expansion for f(x, y) = (x + y)² at (0, 0).

Local Extrema of Real -Valued Functions
We begin with a few basic definitions:

Definition 1.

As you may remember from single-variable calculus, every extremum is a critical point. But
remember that not every critical point is an extremum. This yields the following theorem:

Theorem 1 (First derivative test for local extrema).

From the definition of Df(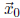), we rephrase the first derivative test as just

Now the next goal is to develop a second-derivative test for multivariable (real-valued) functions.
In general, this second-derivative test is a fairly complicated mathematical object . We introduce
some notation to help us beginning with the Hessian:

Definition 2 (The Hessian).

The Hessian is an example of a quadratic function . These are functions Ø: Rⁿ → R such that



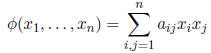
for some values 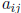. The reason these are called quadratic functions is reflected by the fact that



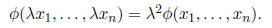
Interpreting a quadratic function in terms of matrix multiplication is useful to know:

Now if we evaluate the Hessian at a critical point 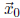of f (i.e. where Df(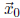) = 0), Taylor’s
theorem tells us

Thus we see that at a critical point, the Hessian is just the first non-constant term in the Taylor
series for f. We want to have a little more notation:

Definition 3 (Positive- and negative-definite).

Observe that if n = 1, we find 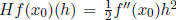, which is positive -definite if and only if
f''(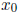) > 0. This fits perfectly with the second -derivative test for single-variable functions and
motivates the following theorem.

Theorem 2 (Second derivative test for local extrema).

In fact the extrema determined by this test are strict in the sense that a local maxima (or minima)
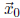is strict if 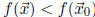(or 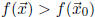) for all nearby .
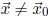In the special case that n = 2, the Hessian for a function f(x, y) is just

We can determine easily a criterion for determining whether a quadratic function given by a 2 × 2
matrix is postive-definite ( or negative -definite):

Lemma 1.

The proof of this lemma is carried out on p. 214-5 and is rather straightforward, so do take a look
at it. We can also arrive at the following formulation :

In fact, similar criteria exist for general n × n symmetric matrices. We consider the n square
submatrices along the diagonal of B:
 

Then B is positive-definite (i.e. the quadratic function defined by B) if and only if

Moreover B is negative-definite if and only if the signs of these sub-determinants alternate between
> 0 and < 0. If all of the sub-determinants are non- zero but the matrix is neither positive- nor
negative-definite, the critical point is of saddle type.

Let us go back to the n = 2 case and restate the second-derivative test in this special case.

Theorem 3 (Second derivative max-min test for functions of two variables).

If D < 0 in this theorem, we will have a saddle point. If D = 0, we will need further analysis
(and will not worry about this situation for now). Critical points for which D ≠ 0 are called
nondegenerate critical points. The remaining critical points, i.e. where D = 0, are called
degenerate critical points and the behavior of the function at those points is determined by
other methods (e.g. level sets or sections).