1. Consider the following system of linear equations.
x + 2y = 8
3x + 4y = 12
a) Write this system of equations in its corresponding matrix form. Write the
augmented matrix
associated with this system of linear equations .
b) Using Gauss- Jordan elimination , determine the solution to this system . [Write
your solution
in vector form.]
c) On a single set of coordinate axes , plot the graphs of the two linear
equations above. Then
label your solution in b ) on the graph . To what does your solution correspond
graphically?
2. Consider the following system of linear equations .
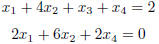
a) Write the augmented matrix associated with this system of equations.
b) Use Gauss- Jordan elimination (also called Gauss-Jordan row reduction) to find
the reduced
echelon form of the augmented matrix. [Indicate clearly the elementary row
operations that you
use . This information will needed in part e.]
c) Write down the system of linear equations whose corresponding augmented
matrix is the
reduced echelon form above.
d) Find the general solution to this system of equations. [Express the general
solution in vector
form.]
e) For each elementary row operation used in b), write down the associated
elementary matrix.
(More questions on next page.)
3. Here is an interesting system of linear equations .
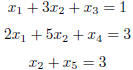
a) Write the augmented matrix associated with this system of equations.
(Observe: Why is it interesting? This particular system is considered reduced
with respect to
the variables 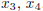 , and
, and
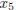 . What this means is
that the columns correponding to the variables
. What this means is
that the columns correponding to the variables
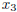 ,
,
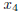 , and
, and
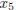 are the columns of an
identity matrix.)
are the columns of an
identity matrix.)
b) Now use Gauss-Jordan elimnation (also called Gauss-Jordan row reduction) to
find the reduced
echelon form of the augmented matrix.
(Observe: The particular system in b) is considered to be reduced with respect
to the variables
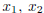 , and
, and 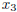 ,
because the columns correponding to the variables
,
because the columns correponding to the variables
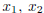 , and
, and 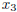 are
the columns
are
the columns
of an identity matrix.)
c) Write down the system of linear equations whose corresponding augmented
matrix is the
reduced echelon form above.
d) Find the general solution to this system of equations. [Express the general
solution in vector
form.]
e) Using your answer in d), find the three specific solutions given by the
following choices of the
free (a.k.a. non-basic) variables.
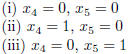
f) Check that your solutions in e) satisfy the original system of linear
equations. Check that they
also satisfy the system of linear equations you gave in c). [If this reveals any
errors, then re-examine
your work in the previous steps .]
(Recall and Observe: By the nature of the elementary row operations, the
solution set of the
original system of equations is the same as the solution set of the transformed
system arising from
elementary row operations. But the transformed system may allow one to make
observations about
the solution set that were not so apparent from the original system.)
g) Challenge question: (We have not exactly covered this yet, but...) Do you
think you could
take your augmented matrix from part b) and reduce it with respect to the
variables 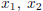 , and
, and
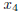 ? Can you reduce it with respect to the
variables
? Can you reduce it with respect to the
variables 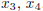 , and
, and
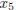 ? (If so, what do you get?)
? (If so, what do you get?)



