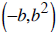Precalculus Review

The following questions review precalculus material from Sections 1.1 – 1.6 of our
textbook, e.g., 1.1.14 refers to Exercise (or Problem) 14 in Section 1.1. I strongly suggest
that you review this material by carefully working each problem on a separate sheet of
paper and then checking your answers (which are provided at the back of this handout).

1. Find the equations of the lines through the point
(a,b) that are parallel and
perpendicular to the line

y = mx + c , assuming

m 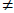0. (1.1.14)

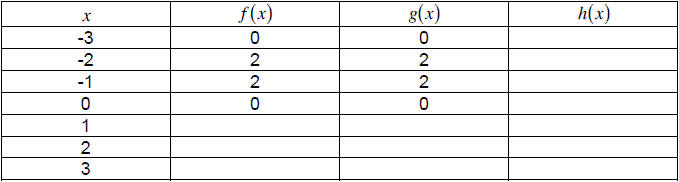
2. The table below shows some values of a linear function f and an
exponential function g. Find exact values (not decimal approximations) for
each of the missing entries. (1.2.38)

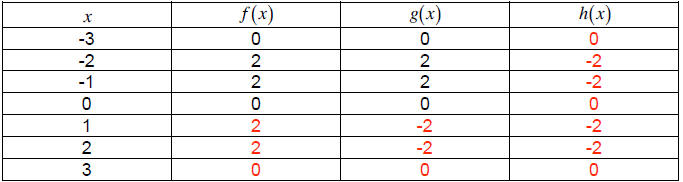
3. Complete the following table with values for the functions f, g, and h, given
that: (1.3.54)

a. f is an even function.
b. g is an odd function.
c. h is the composition h(x) = g( f (x)).

4. At time t hours after taking the cough suppressant hydrocodone bitartrate,
the amount, A, in mg, remaining in the body is given by
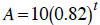. (1.4.40)
a. What was the initial amount taken?
b. What percent of the drug leaves the body each hour?
c. How much of the drug is left in the body 6 hours after the dose is
administered?
d. How long is it until only 1 mg of the drug remains in the body?

5. The Bay of Fundy in Canada has the largest tides in the world. The
difference between low and high water levels is 15 meters (nearly 50 feet).
At a particular point the depth of the water, y meters, is given by the
function of time, t, in hours since midnight by
y = D+ Acos(B(t -C)).
(1.5.38)
a. What is the physical meaning of D?
b. What is the value of A?
c. What is the value of B? Assume the time between successive high tides 12.4 hours.
d. What is the physical meaning of C?

6. The desert temperature, H, oscillates daily between
40°F at 5 am and 80°F at 5 pm. Write a possible formula for H in terms of t , measured in
hours from 5 am. (1.5.44)

7. The height of an object above the ground at time t is given by
,
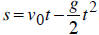where 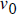is the initial velocity and g is the acceleration due to gravity.
(1.6.20)
a. At what height is the object initially?
b. How long is the object in the air before it hits the ground?
c. When will the object reach its maximum height?
d. What is that maximum height?

8. (1.6.22)
a. If f (x) = ax²+ bx + c , what can you say about the values of a, b,
and c if:

i.(1,1) is on the graph of f (x)?
ii.(1,1) is the vertex of the graph of f (x)? [Hint: The axis of symmetry is
x =-b/(2a).]
iii. The y- intercept of the graph is (0,6).

b. Find a quadratic function satisfying all three conditions.

9. Each planet moves around the sun in an elliptical orbit. The orbital period,
T, of a planet is the time it takes the planet to go once around the sun.
The semimajor axis of each planet's orbit is the average of the largest and
the smallest distances between the planet and the sun. Johannes Kepler
(1571-1630) discovered that the period of a planet is proportional to the 3/2
power of its semimajor axis. What is the orbiting period (in days) of
Mercury, the closest planet to the sun, with a semimajor axis of 58 million
km? What is the period (in years) of Pluto, the farthest planet, with a
semimajor axis of 6000 million km? The semimajor axis of the earth is
150 million km. [Hint: What is the earth's period?] (1.R.44)

10. (1.R.46)
a. Consider the functions graphed in Figure 1.89(a) [pg. 60]. Find the
coordinates of C .
b. Consider the functions in Figure 1.89(b) [pg. 60]. Find the
coordinates of C in terms of b.

Solutions

1. Find the equations of the lines through the point
(a,b) that are parallel and
perpendicular to the line
y = mx + c , assuming
m 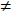0. (1.1.14) Parallel
y = m(x - a) + b, Perpendicular


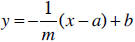
2. The table below shows some values of a linear function f and an
exponential function g. Find exact values (not decimal approximations ) for
each of the missing entries. (1.2.38)

3. Complete the following table with values for the functions f, g, and h, given
that: (1.3.54)
a. f is an even function.
b. g is an odd function.
c. h is the composition h(x) = g( f (x)).

4. At time t hours after taking the cough suppressant hydrocodone bitartrate,
the amount, A, in mg, remaining in the body is given by .
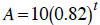(1.4.40)

a. What was the initial amount taken? 10 mg
b. What percent of the drug leaves the body each hour? 18%
c. How much of the drug is left in the body 6 hours after the dose is
administered? Approximately 3.04 mg
d. How long is it until only 1 mg of the drug remains in the body?
Approximately 11.60 hours

5. The Bay of Fundy in Canada has the largest tides in the world. The
difference between low and high water levels is 15 meters (nearly 50 feet).
At a particular point the depth of the water, y meters, is given by the
function of time, t, in hours since midnight by

y = D+ Acos(B(t -C)).
(1.5.38)
a. What is the physical meaning of D? The average depth of water
b. What is the value of A? 7.5
c. What is the value of B? Assume the time between successive high
tides 12.4 hours. pi/6.2 or approximately 0.507
d. What is the physical meaning of C? The time of a high tide

6. The desert temperature, H, oscillates daily between
40°F at 5 am and 80°F at 5 pm. Write a possible formula for H in terms of t, measured in
hours from 5 am. (1.5.44)

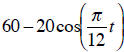
other formulas are possible

7. The height of an object above the ground at time t is given by
,
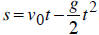where 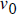is the initial velocity and g is the acceleration due to gravity.
(1.6.20)

a. At what height is the object initially? 0

b. How long is the object in the air before it hits the ground?


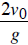
c. When will the object reach its maximum height?


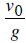
d. What is that maximum height?


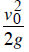
8. (1.6.22)
a. If
f (x) = ax²+ bx + c , what can you say about the values of a, b,
and c if:
i.
(1,1) is on the graph of f (x)? 1= a + b + c

ii.
(1,1) is the vertex of the graph of f (x)? [Hint: The axis of symmetry is
x = -b (2a).] b =-2a or a = c-1 or c = a +1

iii. The y-intercept of the graph is
(0,6).
c = 6

b. Find a quadratic function satisfying all three conditions.
y = 5x²-10x + 6

9. Each planet moves around the sun in an elliptical orbit. The orbital period,
T, of a planet is the time it takes the planet to go once around the sun.
The semimajor axis of each planet's orbit is the average of the largest and
the smallest distances between the planet and the sun. Johannes Kepler
(1571-1630) discovered that the period of a planet is proportional to the
3/2
power of its semimajor axis. What is the orbiting period (in days) of
Mercury, the closest planet to the sun, with a semimajor axis of 58 million
km? Approximately 87.818 days What is the period (in years) of Pluto,
the farthest planet, with a semimajor axis of 6000 million km?
Approximately 253 years The semimajor axis of the earth is 150 million
km. [Hint: What is the earth's period?] (1.R.44)

10. (1.R.46)
a. Consider the functions graphed in Figure 1.89(a) [pg. 60]. Find the
coordinates of C. (-2, 4)
b. Consider the functions in Figure 1.89(b) [pg. 60]. Find the
coordinates of C in terms of b.