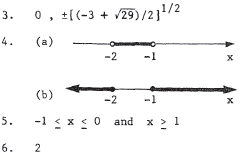REVIEW OF FUNDAMENTALS

R. l Basic Algebra: Real Numbers and Inequalities

PREREQUISITES

1. There are no prerequisites for this section other than some high school
algebra and geometry; however, if the material presented in this section
is new to you, it would be a good idea to enroll in a precalculus course.
This section is intended to be a review.

PREREQUISITE QUIZ

1. Orientation quizzes A and B in the text will help you evaluate your
preparation for this section and this course.

GOALS

1. Be able to factor and expand common mathematical expressions .
2. Be able to complete a square.
3. Be able to use the quadratic formula .
4. Be able to solve equations and inequalities .

STUDY HINTS

1. Common identities. Know how to factor a² - b² . It is a good idea to
memorize the expansion of (a + b)² and (a + b)³ . Note that (a - b)²
can be obtained by substituting -b for 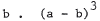can be similarly
expanded. These identities are useful for computing limits in Section 1.2
and Chapter 11 .

2. Factoring. This is a technique that is learned best through practice. A
good starting point is to find all integer factors of the last term (the
constant term). Once you find a factor for the original polynomial, use
long division to find a simpler polynomial to factor. This will be important
for partial fractions in Chapter 10 and for computing limits.

3. Completing the square. Don't memorize the formula. Practice until you
learn the technique. Note that adding ( b/ 2a )² to x² + bx/a forms a
perfect square . This technique will be very important for integration
techniques introduced in Chapter 10.

4. Quadratic formula. - It is recommended that you memorize this formula. It.
is used in many applications in various disciplines such as engineering,
economics, medicine, etc. This formula may also be used to solve equations
of the form Ax⁴ + Bx² + C = 0 by solving for y = x² and taking
square roots to get x .

5. Square roots. Note that, unless otherwise stated, square roots are understood
to be nonnegative. 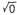is equal to zero.

6. Inequalities. It is essential to have a good handle on manipulating
inequalities. Without this, you will not have a good understanding of
some of the basic theory of calculus. Don't forget to reverse the direction
of the inequality sign when you multiply by a negative number.

SOLUTIONS TO EVERY OTHER ODD EXERCISE

1. 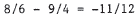is a rational number. Since the denominator cannot
be reduced to one , it is neither a natural number nor an integer.

5. ( a - 3 ) ( b + c ) - ( a c + 2 b ) = ( a b - 3 b + a c - 3 c ) - ( a c + 2 b ) = a b - 5 b - 3 c .

9. We can use Example 2 with b replaced by -b t o get
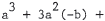
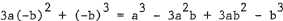. Alternatively , write


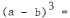
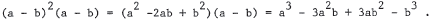
13. We know t h a t (x + a) (x + b) = x² + (a + b)x + ab . The factor s of 6
are 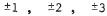, and 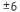. By choosing a = 2 and b = 3 , we
get a + b = 5 . Thus, x² + 5 x + 6 = ( x + 2 ) ( x + 3 ) .

17. First we factor out 3 to get 3(x² - 2x - 8) . We know that the fact-
ors of -8 are 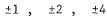, and 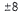. As in Exercise 13, we
look for a and b so that (a + b)x is the middle term. In this case,
a = -4 and b = 2 . Thus, 3x² - 6x - 24 = 3(x - 4 ) ( x + 2 ) .

21. 2(3x - 7) - (4x - 10) = 0 simplifies to (6x - 14) - (4x - 10) =
2x - 4 = 0 , i . e . , 2x = 4 . Dividing by 2 yields x = 2 .

25. The right-hand side is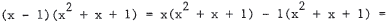
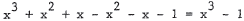, which is the left-hand side.

29. (a) By factoring, we get x² + 5x + 4 = (x + 4) (x + 1) = 0 . If any
factor equals zero, the equation is solved. Thus, x = -4 or x = -1 .

(b) By using the method of completing the square, we get 0 = x² + 5x + 4 =
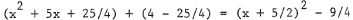. Rearrangement
yields 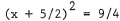, and taking square roots gives
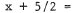
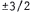. Again, x = -4 or -1 .

(c) a = 1 , b = 5 , and c = 4 , so the quadratic formula

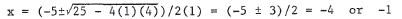
33. We use the quadratic formula with a = -1 , b = 5 , and c = 0.3 .
This gives 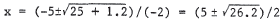. These are the
two solutions for x .

37. x² + 4 = 3x² - x is equivalent to 0 = 2x² - x - 4 . Using the quadratic
formula with a = 2 , b = -1 , and c = -4 , we get


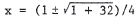
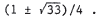
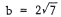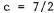41. We apply the quadratic formula with a = 2 , , and to
get 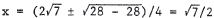. Thus, the only solution is

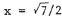
45. We add b to both sides to obtain a + c > 2c . Then we subtract c to
get a > c .

49. b(b + 2) > (b + 1) (b + 2) is equivalent to .
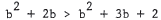Subtracting b² + 2b from both sides leaves 0 > b + 2 . Subtracting 2
yields - 2 > b .

53. (a) Dividing through by a in the general quadratic equation yields
x² + (b/a)x + c/a = 0 . Add and subtract 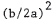to get
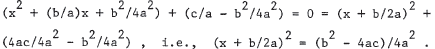Taking
square roots gives 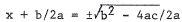, and finally


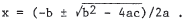
(b) From the quadratic formula, we see that there are no solutions if
b² - 4ac < 0 . If b² - 4ac > 0 , there are two distinct roots.
However, if b² - 4ac = 0 , there are two roots, which both equal
-b/2a . This only occurs if b² = 4ac .

SECTION QUIZ

1. Factor:

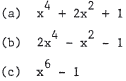
2. Apply the expansion of (a + b)³ t o expand (3x - 2)³ .

3. Use the quadratic formula t o solve x⁵ + 3x³ - 5x = 0 .

4. Sketch the solution of

(a) x² + 3x + 2 < 0
(b) x² + 3x + 2 ≥ 0

5. Find the solution set of .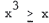

6. The firs t King of the Royal Land of Mathernatica has decreed t h a t the
firs t young lady t o answer the following puzzle shall rule at his side .
The puzzle is t o compute the product of a l l solutions to
x³ + 2x² - x - 2 = 0 . Then, divide by the length of the finite interval
f o r which x³ + 2x² - x - 2 ≥ 0 . What answer would make a lady Queen
of Mathernatica ?*

ANSWERS TO SECTION QUIZ



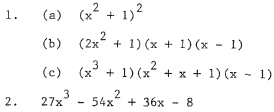
*Dear Reader: I realize that many of you h a t e math but a r e forced t o comp
lete this course for graduation, Thus, I have attempted t o maintain interest
with " entertaining " word problems. They are not meant t o be insulting
to your intelligence . Obviously, most of the situations will never
happen; however, calculus has several practical uses and such examples are
found throughout Marsden and Weinstein's text . I would appreciate your
comments on whether my "unusual" word problems should be kept for the next
edition .