Try the Free Math Solver or Scroll down to Resources!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Linear Algebra Homework 1

Problem 1 - 1ex

Let

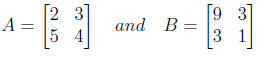
Solve for X the matrix equation

A + 2X = B

Do it first by adding matrices on the left hand side and then comparing the entries of the
resulting matrix and matrix B. Then solve it again using matrix algebra.

Problem 2 - 2ex

(a) Let

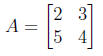
Compute

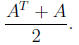
(b) Show that for any square matrix 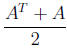is a symmetric matrix.

Problem 3 - 2ex

Let A be a square matrix. For which combinations of scalars α and β the matrix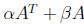
is a symmetric matrix.

Problem 4 - 1ex

Let A and B are two symmetric matrices. Show that A + B is symmetric.

Problem 5 - 1ex

Let A and B are two symmetric matrices. For which combinations of scalars α and β the matrix 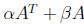is a symmetric matrix.

Problem 6 - 1ex

Let A be a symmetric matrix. Show the matrix αI + A is a symmetric matrix.

Problem 7 - 2ex

Let A and B are two square matrices. Let C = A − B is a symmetric matrix. What does
that tell you about matrices A and B?

Problem 8 - 1ex

A matrix is an upper triangular matrix if all its entries under the diagonal are 0.
Let A and B are two upper triangular matrices. For which combinations of scalars α and β
the matrix 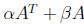is an upper triangular matrix.