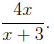Try the Free Math Solver or Scroll down to Resources!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Rational Expressions and Rational Equations

1 Simplifying Rational Expressions

Rational functions are nothing more than fractions whose numerators and denominators are
polynomials. Because they are functions, they have domains. It may not be possible to
evaluate the function at any real number. Because rational functions are fractions, having
the denominator be zero gives us something which is undefined. This gives us the important
idea.

Important Idea. A rational expression is defined exactly where the denominator is not
zero.

Example 1. Determine the values of variable where each expression is defined.

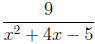
Solution. The function is defined exactly where the denominator is not zero. Therefore, we
find where the denominator is zero and eliminate those possibilities. The denominator will
be zero when

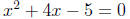
Using the quadratic formula, we have

a = 1, b = 4, c = -5.

The discriminant is then

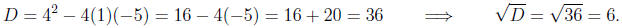
The zeros are then given by

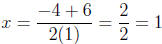and

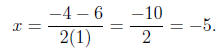
Thus, the domain of the expression will be all real numbers except 1 and -5.

Example 2. Determine the value of the variables where the rational expression is defined.

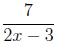
Solution. Again, the expression will be defined where the denominator is not zero. Thus, we
need to solve


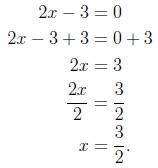	(add 3 to both sides)

	(divide both sides by 2)

Thus the expression will be defined for all real numbers except .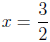

Example 3. Determine the values of the variables where the denominator is defined.

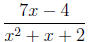
Solution. The expression will be defined where the denominator is not zero. We then find
where the denominator is zero and we eliminate those values. We therefore need to solve

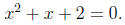
Identifying the coefficients

a = 1, b = 1, c = 2.

Computing the discriminant, we have

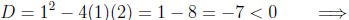no real solutions

Since the denominator is never zero, no values have to be eliminated. This means the function
is defined for all real numbers.

Simplifying rational expressions is exactly like simplifying fractions. You factor the num-berator
and the denominator into primes and the cancel common factors between numerator
and denominator.
Example 4. Simplify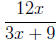

Solution. In the denominator, we can take out a factor of 3.

3x + 9 = 3x + 3(3) = 3(x + 3).

Likewise, in the numerator we can take out a factor of 3 to give us

12x = 3(4x).

In our rational expression we then have

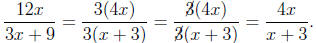
Thus, our simplified expression is