1 Introduction
Continued fractions offer a means of concrete representation for arbitrary real
numbers . The
continued fraction expansion of a real number is an alternative to the
representation of such a
number as a (possibly infinite) decimal .
The reasons for including this topic in the course on Classical Algebra are :
(i) The subject provides many applications of the method of recursion .
(ii) It is closely related to the Euclidean algorithm and, in particular, to
“Bezout’s Identity”.
(iii) It provides an opportunity to introduce the subject of group theory via
the 2-dimensional
unimodular group 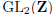 .
.
2 The continued fraction expansion of a real number
Every real number x is represented by a point on the real line and , as such,
falls between two
integers. For example, if n is an integer and
n ≤ x < n + 1 ,
x falls between n and n + 1, and there is one and only one such integer n for
any given real x.
In the case where x itself is an integer, one has n = x. The integer n is
sometimes called the
floor of x, and one often introduces a notation for the floor of x such as
n = [x] .
Examples:
1.  −2 = [−1.5]
−2 = [−1.5]
2.  3 = [ ]
3 = [ ]
For any real x with n = [x] the number u = x − n falls in the unit interval I
consisting of
all real numbers u for which 0 ≤ u < 1.
Thus, for given real x there is a unique decomposition
x = n + u
where n is an integer and u is in the unit interval. Moreover, u = 0 if and only
if x is an
integer. This decomposition is sometimes called the mod one decomposition of a
real number.
It is the first step in the process of expanding x as a continued fraction.
The process of finding the continued fraction expansion of a real number is a
recursive process
that procedes one step at a time. Given x one begins with the mod one
decomposition
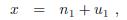
where 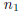 is an integer and
is an integer and 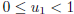 .
.
If 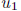 = 0, which happens if and only if x is an
integer, the recursive process terminates with
= 0, which happens if and only if x is an
integer, the recursive process terminates with
this first step. The idea is to obtain a sequence of integers that give a
precise determination
of x.
If 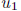 > 0, then the reciprocal 1/
> 0, then the reciprocal 1/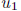 of
of 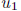 satisfies 1/
satisfies 1/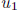 > 1 since
> 1 since 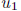 is in I
and, therefore,
is in I
and, therefore,
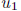 < 1. In this case the second step in the recursive determination of the
continued fraction
< 1. In this case the second step in the recursive determination of the
continued fraction
expansion of x is to apply the mod one decomposition to 1/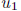 . One writes
. One writes
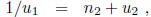
where 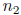 is an integer and 0 ≤
is an integer and 0 ≤
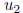 < 1. Combining the equations that represent the
first two
< 1. Combining the equations that represent the
first two
steps, one may write
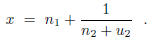
Either 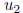 = 0, in which case the process ends with the
expansion
= 0, in which case the process ends with the
expansion
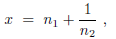
or 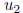 > 0. In the latter case one does to
> 0. In the latter case one does to 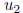 what had just been done to
what had just been done to 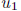 above
under the
above
under the
assumption 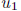 > 0. One writes
> 0. One writes
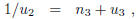
where 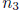 is an integer and 0 ≤
is an integer and 0 ≤
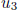 < 1. Then combining the equations that represent
the first
< 1. Then combining the equations that represent
the first
three steps, one may write
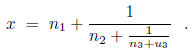
After k steps, if the process has gone that far, one has integers
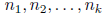 and real numbers
and real numbers
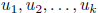 that are members of the unit interval I with
that are members of the unit interval I with
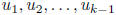 all positive. One
all positive. One
may write
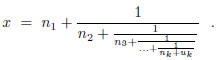
Alternatively, one may write
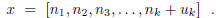
If 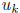 = 0, the process ends after k steps. Otherwise, the process continues at
least one more
= 0, the process ends after k steps. Otherwise, the process continues at
least one more
step with
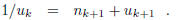
In this way one associates with any real number x a sequence, which could be
either finite or
infinite, 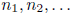 of integers. This sequence is called the continued
fraction expansion of x.
of integers. This sequence is called the continued
fraction expansion of x.
Convention. When 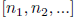 is called a continued fraction, it is understood
that all of the
is called a continued fraction, it is understood
that all of the
numbers 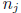 are integers and that
are integers and that
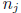 ≥1 for j ≥ 2.
≥1 for j ≥ 2.
3 First examples
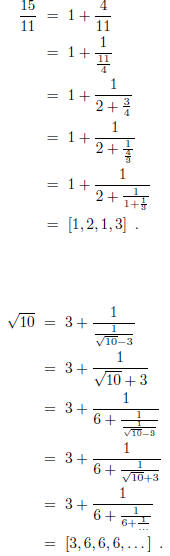
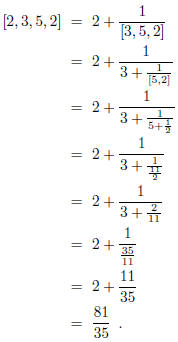
Let
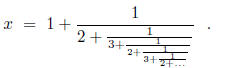
In this case one finds that
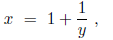
where

Further reflection shows that the continued fraction structure for y is
self-similar:
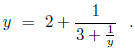
This simplifies to
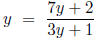
and leads to the quadratic equation
3y2 − 6y − 2 = 0
with discriminant 60. Since y > 2, one of the two roots of the quadratic
equation cannot be
y, and, therefore,
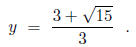
Finally,
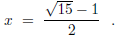
The idea of the calculation above leads to the conclusion that any continued
fraction 
that eventually repeats is the solution of a quadratic equation with positive
discriminant and
integer coefficients. The converse of this statement is also true, but a proof
requires further
consideration.
4 The case of a rational number
The process of finding the continued fraction expansion of a rational number is
essentially
identical to the process of applying the Euclidean algorithm to the pair of
integers given by its
numerator and denominator .
Let x = a/b, b > 0, be a representation of a rational number x as a quotient of
integers a and
b. The mod one decomposition
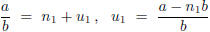
shows that 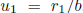 , where
, where
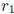 is the remainder for division of a by b. The case
where
is the remainder for division of a by b. The case
where
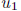 = 0 is the case where x is an integer. Otherwise
= 0 is the case where x is an integer. Otherwise 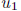 > 0, and the mod one
decomposition
> 0, and the mod one
decomposition
of 1/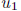 gives
gives
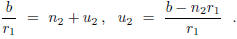
This shows that 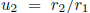 , where
, where
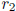 is the remainder for division of b by
is the remainder for division of b by
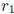 .
Thus, the
.
Thus, the
successive quotients in Euclid’s algorithm are the integers
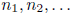 occurring in the continued
occurring in the continued
fraction. Euclid’s algorithm terminates after a finite number of steps with the
appearance of a
zero remainder . Hence, the continued fraction expansion of every rational number
is finite.
Theorem 1. The continued fraction expansion of a real number is finite if and
only if the real
number is rational.
Proof. It has just been shown that if x is rational, then the continued fraction
expansion of x is
finite because its calculation is given by application of the Euclidean
algorithm to the numerator
and denominator of x . The converse statement is the statement that every finite
continued
fraction represents a rational number. That statement will be demonstrated in
the following
section.



