The English System
Originally, a yard was the distance from the tip of the nose to the end of an
outstetched arm of
an adult person and a foot was the length of a human foot. Since then it has
gone through many
definitions until now the definitions are based on the meter.
| Unit |
Equivalent in Other Units |
| yard (yd) |
3 feet |
| foot (ft) |
12 inches |
| mile (mi) |
1760 yards or 5280 feet |
Dimensional Analysis (Unit Analysis)
A process used to convert from one unit of measure to another using unit ratios
( ratios equivalent to 1).
Example 1. Convert each of the following.
a) 200 feet = ____ yards
b) 3.75 yards = ____ inches
c) 8690 feet = ____ miles
d) 940 inches = ____ yards
The Metric System
| Unit |
Symbol |
Relationship to Base Unit |
| kilometer |
km |
1000 m |
| hectometer |
km |
100 m |
| dekameter |
dam |
10 m |
| meter |
m |
base unit |
| decimeter |
dm |
0.1 m |
| centimeter |
cm |
0.01 m |
| millimeter |
mm |
0.001 m |
Approximate Conversions Between English and Metric Systems
•1 kilometer ≈ 0.62 miles
•1 meter ≈ 1.09 yards
•2.54 centimeters ≈ 1 inch
Example 2. Convert each of the following.
a) 3.5 km = ____ m
b) 375 cm = ____ hm
c) 765 mm = ____ dm
d) 5.8 km = ____ cm
e) 70 miles/hour = ____ km/hour
f) 100 yards = ____ meters
Example 3. If our money system used metric prefixes
and the base unit was a dollar, give metric names to
each of the following.
a) dime
b) penny
c) $10 bill
d) $100 bill
e) $1000 bill
Greatest Possible Error.
The greatest possible error (GPE) of a measurement is one-half the smallest
unit used.
Example 4. Determine the GPE for each of the
following measurements and interpret.
a) 25 inches
b) 10.8 cm
c) 5.64 m
Distance Properties
1. The distance between any two points A and B is greater than or equal to 0,
written AB≥0.
2. The distance between any two points A and B is the same as the distance
between B and A, written
AB = BA.
3. For any three points A, B, and C, the distance between A and B plus the
distance between B and C is
greater than or equal to the distance between A and C, written AB+BC≥AC.
Distance Around a Plane Figure
The perimeter of a simple closed curve is the length of the curve. If a figure
is a polygon, its
perimeter is the sum of the lengths of its sides. A perimeter has linear
measure .
Example 5. Find the perimeter of each of the shapes
below.
Example 6. Given a square of any size, stretch a
rope tightly around it. Now take the rope off, add 100 inches
to it, and put the extended rope back around the square so that the new rope
makes a square around the
original square . Find d, the distance between the squares.
Circumference of a Circle
A circle is defined as the set of all points in a plane that are the same
distance from a given point,
the center. The perimeter of a circle is its circumference.
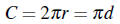
where r is the radius, d is the diameter, and
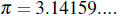
Example 7. Find the circumference of the circle
pictured below.
Arc Length
The length of an arc depends on the radius of the circle and the central angle
determing the arc.
Example 8. Determine the length of each arc
described below of a circle with radius r.
a) Semi-circle
b) Quarter Circle
c) Arc with central angle θ.
Example 9. Find the following.
a) the radius of a circle that has a circumference of 18π
meters.
b) the length of a 35°
arc of a circle with radius 15 cm.
c) the radius of a circle that has an arc with central angle 85°
and length of 150 cm.



