A.2 Pythagoras's theorem in Babylonian mathematics
In this section we examine four Babylonian tablets which all have some
connection
with Pythagoras's theorem. Certainly the Babylonians were familiar with
Pythagoras'
theorem. A translation of a Babylonian tablet which is preserved in the British
museum goes as follows
4 is the length and 5 the diagonal. What is the breadth?
Its size is not known.
4 times 4 is 16.
5 times 5 is 25.
You take 16 from 25 and there remains 9.
What times what shall I take in order to get 9?
3 times 3 is 9.
3 is the breadth.
All the tablets come from roughly the same period, namely that of the Old Baby-
lonian Empire which flourished in Mesopotamia between 1900 BC and 1600 BC.
The four tablets which interest us here we will call the Yale tablet YBC 7289,
Plimpton 322, the Susa tablet, and the Tell Dhibayi tablet. Let us say a little
about
these tablets before describing the mathematics which they contain.
The Yale tablet YBC 7289 which we describe is one of a large collection of
tablets
held in the Yale Babylonian collection of Yale University. It consists of a
tablet on
which a diagram appears. The diagram is a square of side 30 with the diagonals
drawn in . The tablet and its significance was first discussed in Neugebauer5 and
in
Fowler and Robson.
Plimpton 322 is the tablet numbered 322 in the collection of G A Plimpton housed
in Columbia University. The top left hand corner of the tablet is damaged as and
there is a large chip out of the tablet around the middle of the right hand
side. Its date
is not known accurately but it is put at between 1800 BC and 1650 BC. It is
thought
to be only part of a larger tablet, the remainder of which has been destroyed,
and at
first it was thought to be a record of commercial transactions. However
Neugebauer
and Sachs gave a new interpretation and since then it has been the subject of a
huge
amount of interest.
The Susa tablet was discovered at the present town of Shush in the Khuzistan
region of Iran. The town is about 350 km from the ancient city of Babylon. W.
K. Loftus identified this as an important archaeological site as early as 1850
but
excavations were not carried out until much later. This particular tablet
investigates
how to calculate the radius of a circle through the vertices of an isosceles
triangle.
Finally the Tell Dhibayi tablet was one of about 500 tablets found near Baghdad
by archaeologists in 1962. Most relate to the administration of an ancient city
which
flourished in the time of Ibalpiel II of Eshunna and date from around 1750 BC.
The
particular tablet in which we are interested is not one relating to
administration but
one which presents a geometrical problem which asks for the dimensions of a
rectangle
whose area and diagonal are known.
Before looking at the mathematics contained in these four tablets we should say
a
little about their significance in understanding the scope of Babylonian
mathematics.
First, you must be careful not to read into early mathematics any ideas which we
can
see clearly today yet which were never in the mind of that author. Conversely,
we
must be careful not to underestimate the significance of the mathematics just
because
it has been produced by mathematicians who thought very differently from today's
mathematicians. As a final comment on what these four tablets tell us of Babylo-
nian mathematics we must be careful to realize that almost all of the
mathematical
achievements of the Babylonians, even if they were all recorded on clay tablets,
have
been lost and, even if these four may be seen as especially important among
those
surviving, they may not represent the best of Babylonian mathematics.
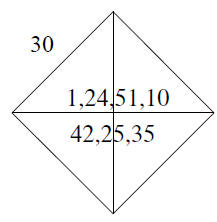
There is no problem understanding what the Yale tablet YBC 7289 is about - a
diagram is on the right.
It has on it a diagram of a square with 30 on one
side, the diagonals are drawn in and near the center
is written 1, 24, 51, 10 and 42, 25, 35. These are num-
bers are written in Babylonian numerals to base 60.
The Babylonian numbers are always ambiguous and
no indication occurs as to where the integer part ends
and the fractional part begins. Assuming that the first
number is 1; 24, 51, 10 then converting this to a decimal
gives 1.414212963 while 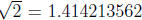 . Calculat- . Calculat-
ing 30×1; 24, 51, 10 gives 42; 25, 35 which is the second
number. The diagonal of a square of side 30 is found
by multiplying 30 by the approximation to 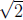 . . |
 |
This shows a nice understanding of Pythagoras's
theorem. However, even more significant is the ques-
tion how the Babylonians found this remarkably good
approximation to 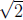 . Several authors conjecture
that the Babylonians used a
. Several authors conjecture
that the Babylonians used a
method equivalent to Heron 's method. The suggestion is that they started with
a guess, say x. They then found e = x2 - 2 which is the error. Then
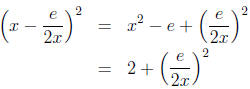
and they had a better approximation since if e is small
then (e/2x)2 will be very
small. Continuing the process with this better approximation to
 yields a still
yields a still
better approximation and so on. In fact as Joseph points out, you need only two
steps
of the algorithm if you start with x = 1 to obtain the approximation 1; 24, 51,
10.
This is certainly possible and the Babylonians' understanding of quadratics adds
some weight to the claim. However there is no evidence of the algorithm being
used in
any other cases and its use here must remain no more than a fairly remote
possibility.
E. F. Robertson suggests an alternative. The Babylonians produced tables of
squares, in fact their whole understanding of multiplication was built round
squares,
so perhaps a more obvious approach for them would have been to make two guesses,
one high and one low say a and b. Take their average (a + b)/2 and
square it. If the
square is greater than 2 then replace b by this better bound, while if the
square is less
than 2 then replace a by (a + b)/2. Continue with the algorithm. Now this
certainly
takes many more steps to reach the sexagesimal approximation 1; 24, 51, 10. In
fact
starting with a = 1 and b = 2 it takes 19 steps as the table below shows:
|
step |
decimal
approx |
sexagesimal
approx |
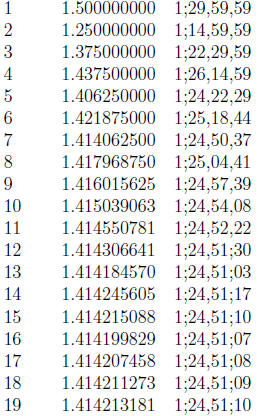 |
The Babylonians were not afraid to undertake a computation
and they may have
been prepared to continue this straightforward calculation until the answer was
correct
to the third sexagesimal place.
Next we look again at Plimpton 322 The tablet has four columns with 15 rows.
The last column is the simplest to understand for it gives the row number and so
contains 1, 2, 3, ... , 15. The remarkable fact which Neugebauer and Sachs
pointed
out is that in every row the square of the number c in column 3 minus the square
of
the number b in column 2 is a perfect square , say h.
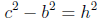
So the table is a list of Pythagorean integer triples. Now
this is not quite true since
Neugebauer and Sachs believe that the scribe made four transcription errors, two
in
each column and this interpretation is required to make the rule work. The
errors are
readily seen to be genuine errors, however, for example 8, 1 has been copied by
the
scribe as 9, 1. The first column is harder to understand, particularly since
damage to
the tablet means that part of it is missing. However, using the above notation,
it is
seen that the first column is just (c/h)2.
So far so good, but if one were writing down Pythagorean triples one would find
much easier ones than those which appear in the table. For example the
Pythagorean
triple (3, 4, 5) does not appear, nor does (5, 12, 13) and in fact the smallest
Pythagorean
triple which does appear is (45, 60, 75) (15 times (3, 4, 5)). Also the rows do
not ap-
pear in any logical order except that the numbers in column 1 decrease
regularly. The
puzzle then is how the numbers were found and why are these particular
Pythagorean
triples are given in the table. Several historians (see for example Calinger)
have sug-
gested that column 1 is connected with the secant function. However, as Joseph
comments
This interpretation is a trifle fanciful.
Zeeman has made a fascinating observation. He has pointed out that if the Babylo-
nians used the formulas h = 2mn, b = m2 -n2, c = m2
+n2 to generate Pythagorean
triples then there are exactly 16 triples satisfying n ≤ 60, 30°≤ t ≤45°, and
tan2t = h2/b2 having a finite sexagesimal
expansion (which is equivalent to m, n, b
having 2, 3, and 5 as their only prime divisors). Now 15 of the 16 Pythagorean
triples
satisfying Zeeman's conditions appear in Plimpton 322. Is it the earliest known
math-
ematical classification theorem? Are we now reading too much into the
mathematics
of the Babylonians, though.
To give a fair discussion of Plimpton 322 we should add that not all historians
agree that this tablet concerns Pythagorean triples. For example Exarchakos
claims
that the tablet is connected with the solution of quadratic equations and has
nothing
to do with Pythagorean triples, "we prove that in this tablet there is no
evidence
whatsoever that the Babylonians knew the Pythagorean theorem and the Pythagorean
triads." According to E.F. Robertson there are numerous tablets which show that
the
Babylonians of this period had a good understanding of Pythagoras's theorem.
Other
authors, although accepting that Plimpton 322 is a collection of Pythagorean
triples,
have argued that they had, as Viola9 writes a practical use in giving a,
"general
method for the approximate computation of areas of triangles."
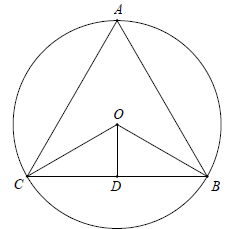
The Susa tablet sets out a problem about an isosceles triangle with sides 50, 50
and 60. The problem is to find the radius of the circle through the three
vertices.
Here we have labeled the triangle A, B, C and the
center of the circle is O. The perpendicular AD is
drawn from A to meet the side BC. Now the triangle
ΔABD is a right angled triangle so, using Pythagoras'
theorem AD2 = Ab2 - BD2, so AD = 40.
Let the
radius of the circle be x. Then AO = OB = x and
OD = 40 - x. Using Pythagoras's theorem again on
the triangle ΔOBD we have x2 = OD2 + Db2.
So
x2 = (40 - x)2 + 302 giving x2
= 402 - 80x + x2
+ 302
and so 80x = 2500 or, in sexagesimal, x = 31; 15. |
 |
Finally consider the problem from the Tell Dhibayi
tablet. It asks for the sides of a rectangle whose area
is 0, 45 and whose diagonal is 1, 15. Now this to us is
quite an easy exercise in solving equations. If the sides
are x and y we have xy = 0:75 and x2 + y2 = (1.25)2.
We would substitute y = 0.75/x into the second equation to obtain a quadratic in
x2 which is easily solved. This however is not the method of solution
given by the
Babylonians and really that is not surprising since it rests heavily on our
algebraic
understanding of equations. The way the Tell Dhibayi tablet solves the problem
is
actually much more interesting than the modern method.
Here is the method from the Tell Dhibayi tablet. We preserve the modern notation
x and y as each step for clarity but we do the calculations in sexagesimal
notation (as
of course does the tablet). Compute 2xy = 1; 30. Subtract from x 2 +y2
= 1; 33, 45 to
get x2+y2-2xy = 0; 3, 45. Take the square root to obtain
x-y = 0; 15. Divide by 2 to
get (x-y)/2 = 0; 7, 30. Divide x 2+y2-2xy = 0; 3, 45 by 4
to get x2/4+y2/4-xy/2 =
0; 0, 56, 15. Add xy = 0; 45 to get x2/4+y2/4+xy/2 = 0;
45, 56, 15. Take the square
root to obtain (x + y)/2 = 0; 52, 30. Add (x + y)/2 = 0; 52, 30 to (x - y)/2 =
0; 7, 30
to get x = 1. Subtract (x-y)/2 = 0; 7, 30 from (x+y)/2 = 0; 52, 30 to get y = 0;
45.
Hence the rectangle has sides x = 1 and y = 0; 45. Remember that this piece of
mathematics is 3750 years old.



