We want to show that the centripetal acceleration for a
particle in uniform circular motion
is
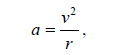
and directed towards the center of the circle . Here v is
the (constant) speed and r the
radius of the circle . In this derivation, we will not need any calculus; we
will, however,
need a fair amount of algebra and geometry .
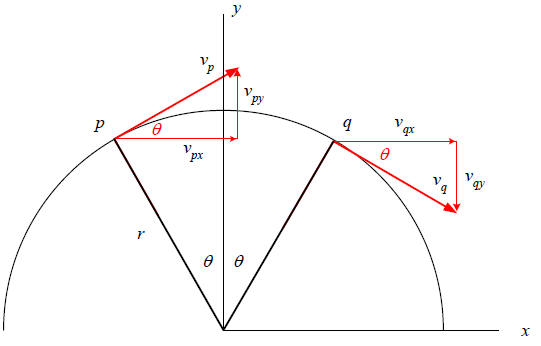
Strategy: In the diagram shown above, assume that the particle moves from
p to q in a
time Δt seconds, at a constant speed v. We will calculate the average
acceleration, and
then take the limit as Δt →0 .
1. First, that as the particle moves from p to q, it moves
a distance arc( pq) , where θ is
measured in radians. Now recall the definition of angle: In the drawing below ,
if s is
arc length and r is the radius of a circle , then by definition
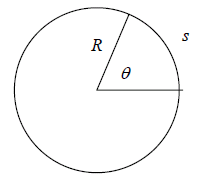 |
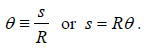
Hence in our case, in the first drawing , the length
of the
arc from p to q is
arc (pq) = r (2θ ) . |
Since the particle is moving at a constant speed v, we can
find the time Δt it takes to
move from p to q using the notion that distance = constant speed × time:
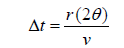
2. We now find the x and y components of the average
acceleration as the particle
moves from p to q. First the x component (the overhead bar means “average”):
final initial
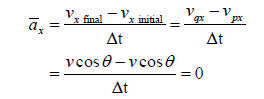
where in the second line I have written x v in terms of the speed v and the
angle θ.
It’s not hard to see from the diagram that the average x-component of the
acceleration
is zero .
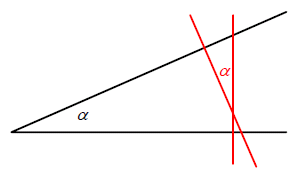
Note: Be sure you understand why the all the angles in the
first drawing are the
same —in terms of my drawing, why the angles shown in black are equal to those
shown in red. It’s an example of the mutual perpendiculars theorem:
Suppose two lines intersect at an angle
α.
Draw lines perpendicular to the original
lines (red in diagram)— then the two
new lines also meet at an angle α.
3. Now the y component of the acceleration:
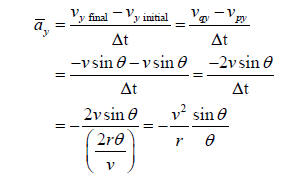
where in the third line I have substituted for Δt from above, and simplified.
Notice
the negative sign —it means that the average acceleration is down. Note: Here is
where we are showing that the acceleration is directed toward the center of the
circle.
4. Finally, we take the limit as Δt →0 . Equivalently , we
can let θ →0 . But now we
can use a well-known theorem from calculus:
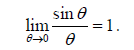
We can find this result numerically : Set your calculator
to radian mode and try
calculating sin θ/θ for smaller and smaller angles. Those of you who have studied
Taylor’s series expansions will also know the result
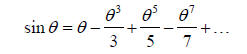
from which our result follows immediately. Hence we know
that in the limit, the
acceleration is
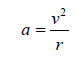
and directed to the center of the circle: QED!