Factoring

I. Greatest Common Factor. Always check to see if you can factor out the greatest common factor (GCF).
The greatest common factor is the largest factor that is shared by all the terms in the given expression. The
GCF may include variables. Also, the GCF sometimes contains more than one term.

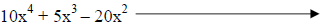	The GCF is 5x2.
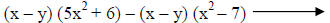	The GCF is (x – y).

After you determine the GCF, you may use the distributive property to rewrite the expression with the GCF
factored out.

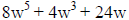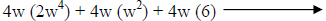	Recognize 4w as the GCF.
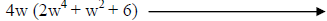	Use distributive property to write in factored form.

Now we will consider three types of polynomials: binomial expressions (two terms), trinomial expressions
(three terms), expressions with four terms. The first step for all these cases will be to factor out the GCF.

II. Binomials. There are three special cases that fall under the two-term category.

A. Difference of squares. A² – B² = (A + B) (A – B)
This may be verified by multiplying out
the right hand side.

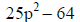	This step may help you to see what the bases are
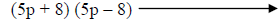	Use the formula to rewrite in factored form.

B. Difference of cubes. A³ – B³ = (A – B) (A² + AB + B²)
Again, this may be verified by
multiplying out the right hand side.

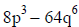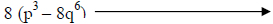	Factor out the GCF first.
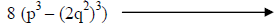	Recognize the difference of cubes.
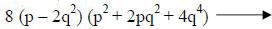	Write in factored form using the difference of cubes formula.

C. Sum of cubes. A³ + B³ = (A + B) (A2 – AB + B²)

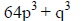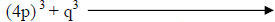	Recognize the sum of cubes.
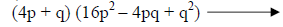	Write in factored form using the sum of cubes formula.

Note: There is no factorization for the sum of squares. For example, 9p²+ 4q² cannot be factored. It is
prime.

III. Trinomials. We will discuss two different ways to factor a trinomial of the form ax²+bx+c.

A. The ac method or grouping method.
1. This is sometimes called the ac method because with trinomials of the form ax²+bx+c (where a,
b, c are constants) the first step will be to multiply a and c.
2. Next, you will look for two factors of the product “ac” that add to form the middle term’s
coefficient, “b” of the original trinomial.
3. Then you rewrite the middle term as the sum of those two factors you discovered in step 2. Don’t
forget to include the variable (they are like terms and need to be like the original middle term).
4. Now you have a four-term polynomial. Group the expression into two groups of two terms each
and factor out the GCF for each 2-term group. (This grouping step is the reason why we
sometimes call this the grouping method.)
5. You should now recognize a common binomial factor. Factor this binomial out and write the
expression in factored form by using the distributive property.

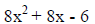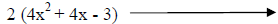	First factor out the GCF. Then multiply “a” and “c.” (4)(-3) = -12 Two factors of -12 that add to form 4 are -2 and 6.
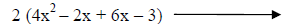	Rewrite the middle term as the sum of “–2x” and “6x.”
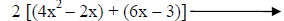	Group the four terms into two groups of two.
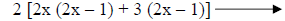	Factor out the GCF for each group and recognize (2x – 1) is the common binomial factor.
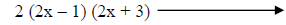	Use the distributive property to write in factored form.

B. Trial and error method. This method involves finding factors of the leading term (the “a”) and the last
term (the “c”) and trying them out in the product of two binomials. Use FOIL to multiply and see if the
factors in your trial produce the original trinomial.

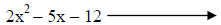	Factors of 2 are 1&2. Factors of -12 are 1&-12, -1&12, 2&-6, -2&6, 3&-4, -3&4.
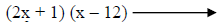	Trying 1&-12.
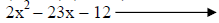	FOIL shows that this trial doesn’t work
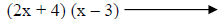	Trying 4&-3.
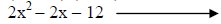	FOIL shows this doesn’t work.
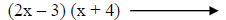	Trying -3&4.
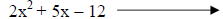	FOIL shows this doesn’t work (but we are close, let’s try 3&-4).
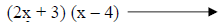	Trying 3&-4.
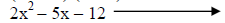	This one works.
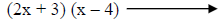	Answer.

Note: The trial and error method may seem like an arduous task, but the more you practice the faster
you’ll get (eventually doing the FOIL part in your head).
Note also: The trial and error method is usually the better of the two methods to use if the leading
coefficient of the trinomial is a one.

IV. Expressions with four terms.

A. Group the expressions into two groups of two terms each.
B. Factor out the GCF of each group.
C. Recognize the common factor and use distributive property.

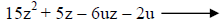	Group the terms. We’ll try grouping the first two and the last two.
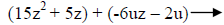	Notice when we grouped the second two terms, we were careful to put the negative in front of the “6uz” term inside the second parenthesis and put a plus sign in between the two sets of parentheses. If we group like this: (15z2 + 5z) – (6uz – 2u) we have changed the original expression!
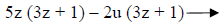	Factor out GCFs for each group. Note that we could factor out a positive or negative “2u” out of the second group. We factored out a negative, so that the signs for the binomial part in parentheses will match.
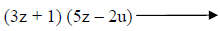	Recognize (3z + 1) is a common factor and use the distributive property to write in factored form.

Note: If you try grouping the first two terms and last two terms and it doesn’t work, the commutative
property of addition allows us to try a different grouping (like the first and third in one group and
the second and fourth in the other). For an expression with four terms, there are three different
possible groupings.

Note also: You may be able to use the four-term grouping method for expressions with more than four
terms. For example, you may try grouping a five-term expression into a difference of squares
and a trinomial. Then apply the techniques discussed above for each of these groupings and
look for a common factor.

Note as well: Remember to factor completely. For instance, you may have to use difference of squares
more than once to get a completely factored form.

Note additionally: Factoring can be used to solve quadratic equations of the form ax²+bx+c = 0 (this is the
standard form of a quadratic equation). The process will be to set the quadratic equation
equal to zero (put it in standard form) and then factor it. Then you will use the zero-
product property, which states: if AB=0, then A=0 or B=0 (or they both equal zero).

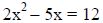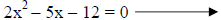	Subtract 12 from both sides of the equal sign to get the quadratic equation in standard form.
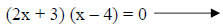	Factor (see discussion on factoring trinomials).
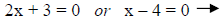	Use the zero product property and set each factor to zero.
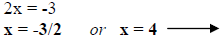	There are two solutions. You may check these by plugging them into the original quadratic equation.
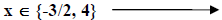	Answer (this form is called set notation; ∈ means “is an element of”).