Try the Free Math Solver or Scroll down to Resources!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Negatives,Mixed Numbers and Improper Fractions

1. Compute 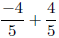algebraically. Justify each equality.

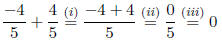
(i) Addition in Q
(ii) Addition in Z
(iii) 0 as a fraction

2. Compute 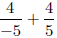algebraically. Justify each equality.

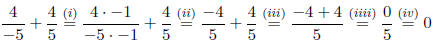
(i) Fundamental Law
(ii) Multiplication in Z
(iii) Addition in Q
(iiii) Addition in Z
(iv) 0 as a fraction

3. Compute 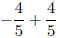algebraically. Justify each equality.
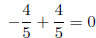by definition of negative numbers.

4. Use fundamental law to show

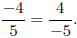
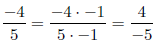
5. Use fundamental law to show

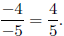
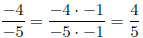
6. Explain why you cannot use fundamental law to show
.
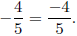
The negative sign on −4/5 is out in front of the fraction and is not attached to either the numerator or
denominator. The Fundamental Law of Fractions will only change the numerator and denominator, it will
never change the negative sign out in front of the fraction.

7. Show algebraically that 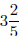equals 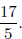Justify each equality.

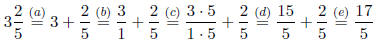
(a) Definition of Mixed number
(b) Integer in rational form
(c) Fundamental Law
(d) Multiplication in Z
(e) Addition in Q

8. (a) You probably would not have a student convert a mixed number to an imporoper fraction in the way
you did in problem 7. Explain to a student the standard algorithm to convert a mixed number to an
improper fraction.

Step 1: Multiply the denominator by the whole number.
Step 2: Add the above product to the numerator.
Step 3: Put the above sum as the numerator of your new fraction, keeping the denominator the same.
In other words, if 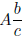is the mixed number then the improper fraction is

(b) Explain why the algorithm you gave above works.
Let’s consider the mixed number 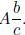Since c is the denominator we know a whole is broken into c
pieces. Let’s break each of the A wholes into c pieces, which means the wholes now have a total of Ac
shaded pieces. The b tells us that there are b shaded pieces in the last whole. Therefore we have a total
of Ac + b shaded pieces. Therefore we know the numerator is Ac + b. In addition, each of the wholes
has c pieces in it, so the denominator is still c. Thus we have the fraction
.
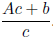
9. Explain to a student the standard algorithm to convert an improper fraction to a mixed number.
Step 1: Divide the denominator into the numerator.
Step 2: The quotient is the whole number.
Step 3: The remainder is the numerator.
Step 4: The denominator remains the same.

10. Explain why the algorithm you gave above works
The denominator tells us how many pieces it takes to make a whole, so dividing the denominator into the
numerator tells us how many wholes we have. The remainder tells us how many pieces are left over, which
becomes the numerator. The pieces are still the same size, so the denominator stays the same.

11. You give Max the problem 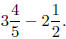Max does the problem in the following way.
3 − 2 = 1

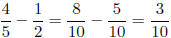
Therefore Max concludes that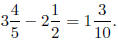
(a) Is Max’s answer correct? Yes
(b) Is Max’s method correct? Explain.
Yes, we can rewrite subtraction as addition of negatives, then uses associative and commutaive properties
of addition. See below.

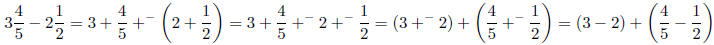
12. You then give Max the problem 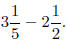He tries to do it the same way, but gets confused.
(a) What could be confusing Max?
Max probably got confused because when he subtracts the fractional parts, he gets a negative.
(b) What can you say to help him?
Using his method he would get 1 for the whole number part and − 3/10 for the fractional part. So he
need only compute 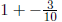to get the correct answer.