Multiplying and Dividing Fractions and Mixed Numbers
PURPOSE
The knowledge of multiplying and dividing fractions will
be used often in your daily life. Whether
you are purchasing floor covering, material for four bridesmaids' dresses, or
figuring out the amount
and size of lumber for a particular project, there are many activities that
require the multiplication
and division of fractions.
OBJECTIVES
After completing this lesson, you should be able to
• multiply fractions and mixed fractions;
• divide fractions and mixed fractions; and
•use multiplication and division of fractions in real-life situations.
READING ASSIGNMENT
Textbook, Chapter 6
COMMENTARY
Section 1: Multiplying Fractions
To multiply fractions, you must multiply the numerators
and denominators, respectively. The new
fraction must then be reduced into its lowest terms.
| Complete Think and Discuss problems 1–5 on page
130. Complete exercises 7–59 odd and 61–77 on page 131. Check your answers with those provided in Appendix A. |
If you feel that you need additional practice multiplying
fractions, you may complete the Extra
Practice problems for this section on page 418 in your textbook (answers are
provided in Appendix
B).
Section 2: Multiplying Fractions: A Shortcut
My guess is that you have probably already been using this
shortcut. If not, I encourage you to use it
faithfully. The process will reduce the effort required to do these problems and
make them more
enjoyable. I love this section for just that reason. The procedure requires the
reduction of the
numerator and the denominator with a common factor to its lowest terms before
multiplying the
numerators and denominators together.
| Complete Think and Discuss problems 1–4 on page
132. Complete Exercises 5–49 odd and 50–66 on page 133. Check your answers with those provided in Appendix A. |
If you feel that you need some additional practice using
the shortcut when multiplying fractions, you
may complete the Extra Practice problems for this section on page 419 in your
textbook (answers are
provided in Appendix B).
Section 3: Using Guess and Check to Solve Problems
By focusing on specific mathematical procedures in math
class, teachers often forget that trial and
error is a perfectly good skill and should be stressed more. At times it takes
longer to solve the
problem, but more often than not trial and error is a valid technique.
| Complete problems 1–9 on page 135. Check your answers with those provided in Appendix A. |
Section 4: Multiplying Mixed Numbers
The first step in multiplying mixed numbers is to adjust
each number to an improper fraction. Next,
use the multiplication process discussed in previous sections. Remember to
reduce the fractions
before multiplying.
| Complete Think and Discuss problems 1–5 on page
136. Complete Exercises 7–39 odd and 40–51 on page 137. Check your answers with those provided in Appendix A. |
If you feel that you need more practice multiplying mixed
numbers, you may complete the Extra
Practice problems for this section on page 419 in your textbook (answers are
provided in Appendix
B).
Section 5: Estimating Products of Fractions and Mixed Numbers
No doubt you have been in a store and discovered the need
to multiply fractions but had no paper
and pencil. In this instance, the process of estimating becomes invaluable.
There are two methods
that can be used when estimating. The first involves rounding the top
multiplication and the bottom
product into multiples of 10, making the reducing easier. The second method
involves estimating a
simpler fraction—such as one-half or one-fourth the whole number—and completing
the
computation with the simpler approximation.
| Complete problems 1–6 on pages 138–139. Complete Exercises 7–21 odd and 22–33 on page 139. Check your answers with those provided in Appendix A. |
Section 6: Dividing Fractions
When dividing one fraction by another, it is important to
multiply the fraction to the left by the
reciprocal of the divisor (the fraction to the right). Dividing fractions is
really just multiplying them
after flipping the divisor. As you work through this process, remember that when
dividing by a
fraction less than 1 you will get a bigger number. For example, if you have a
candy bar and divide it
into halves, you would have two pieces.
| Complete Think and Discuss problems 1–6 on pages
140–141. Complete Exercises 7–43 odd and 45–51 on page 141. Check your answers with those provided in Appendix A. |
If you feel that you need additional practice dividing
fractions, you may complete the Extra Practice
problems for this section on page 420 in your textbook (answers are provided in
Appendix B).
Section 7: Dividing Mixed Numbers
Just as in multiplication, the first step in dividing
mixed numbers is to rewrite each mixed fraction as
an improper fraction. Next, flip the right fraction, reduce, and multiply. In
problems in which you
begin with mixed fractions, your answer should, in most cases, be converted to a
mixed fraction.
| Complete Think and Discuss problems 1–5 on page
142. Complete Exercises 7–49 odd and 51–64 on page 143. Check your answers with those provided in Appendix A. |
If you feel that you need extra practice in dividing mixed
numbers, you may complete Extra Practice
problems for this section on page 420 in your textbook (answers are provided in
Appendix B).
Section 8: Fractions: A Business Application
Fractions are commonly used in the business world. Some of
the processes that are used include
multiplying decimals and whole numbers, rounding quotients, rounding to the
nearest cent, and
multiplying fractions by decimals. The example below illustrates the process of
multiplying fractions
by decimals.
Start with the problem:
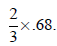
Place decimal over 1:
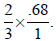
Multiply numerators and denominators:
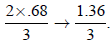
Then divide:
.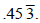
Finally, round to nearest cent:
.45.
| Complete Think and Discuss problems 1–14 on pages
144–145. Complete Review problems 15–22 on page 145. Check your answers with those provided in Appendix A. |



