Try the Free Math Solver or Scroll down to Resources!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Polynomials in Several Variables

§ 6.4 Polynomials in Several
Variables – Objectives (p352)

1. Evaluate polynomials in several
variables.

2. Understand the vocabulary of
polynomials in two variables.

3. Add and subtract polynomials in
several variables.

4. Multiply polynomials in several
variables.

§ 6.4 Obj # 1 Evaluate polynomials
in several variables: p352-353

P358#82 The storage shed shown in the
figure has a volume given by the
polynomial

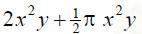
P358#82 a. A small businesss is

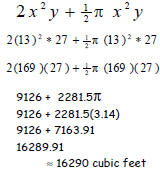
• This is the given polynomial
• Replace x by 13 and y by 27
• Evaluate the exponential
expressions first!

x² = 13² = (13)(13) = 169
(avoid the temptation to do
2(13) = 26 first!)

• Perform indicated
multiplication.
• This is the EXACT answer,
but it’s not practical!
• π is approx. 3.14

• Need to answer in a sentence!
The volume of the storage shed is
about 16290 cubic feet.
• Note: Use the π button on your
calculator. It carries π out to more
decimal places-how does it effect
your answer?
• 9126 + 2281.5π Why is this NOT
11407.5 π?

b) The business requires at least
18,000 cubic feet. Should they
construct the storage shed
described in part a?

Evaluating a polynomial in several
variables.
1. Substitute the given value for each
variable
2. Perform the resulting computation
using the order of operations.
(Especially remember to do exponents
before multiplication! Then
multiplication before addition)

§ 6.4 Obj # 2 Understand the
vocabulary of polynomials in two
variables-p352-353

In general, a polynomial in two variables, x
and y, contains the sum of one or more
monomials in the form axⁿy^m. The constant
a is the coefficient. (KNOW THIS!)

The exponents n and m represent whole
numbers. The degree of the monomial
axⁿy^m is n+m.
(Nice to know-will not be tested on this)

§ 6.4 Obj # 3 Add and Subtract
polynomials in several variablesp353-
354

Adding and subtracting polynomials in 2
variables, is the same as in one variable.

Add: Just combine like terms. (Same
variables with same exponents!)

Subtract: Distribute the subtraction
sign to every term of the polynomial
being subtracted. (Change all its signs!)
Then add.

§ 6.4 Obj # 4 Multiplying
Monomials-p354-355

Multiplying Monomials

To multiply monomials, multiply the
coefficients and add the exponents
on variables with the same base.

Example 5 p355

Multiply: (7x²y)(5x³y²)

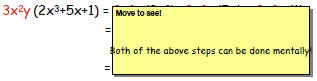
§ 6.4 Obj # 4 Multiplying a
Monomial and Poly-p355

Same as with one variable! We use the
distributive property to multiply a
monomial and a polynomial that is not
a monomial. For example:

§ 6.4 Obj # 4 Multiplying Polynomials in
Two Variables-Same as one variable! p355

The Square of a Binomial Sum

(6x + 4y)² = 36x² + 2(24)xy + 16y ²
= 36x ² + 48xy + 16y ²

The Square of a Binomial Difference

(9x - 3y)² = 81x ² – 2(27)xy + 9y ²
= 81x ² – 54xy + 9y ²

Product of a Sum & Difference of Two Terms

(5x + 3y) (5x - 3y) = 25x ² - 9y ²

Consider the equation of motion for an object tossed straight
up into the air (projected vertically)-or dropped (falling) p359)

s = -½ g t² + v_o t + s_o where:

s is vertical position (height above ground)
of the tossed object in feet (ft)

t is time in seconds that the object has
been in motion (sec)
g is acceleration due to gravity = 32 ft/sec^2
v_o is original speed in ft/sec of object
s_o is original position (i.e. at t = 0) of object

This figure shows that a ball is thrown straight up
from a roof top at an original (initial) velocity of 80
ft/sec from an original (initial) height of 96 feet
above the ground. The ball missed the rooftop on
its way down and eventually strikes the ground

s = -½ g t² + v_o t + s_o
g = 32, v_o = 80 s_o = 96
So the above very general formula becomes a
little more specific for an object with this
original velocity starting at this height:
s = - 16t² + 80 t + 96

For an object with an original velocity original
(initial) velocity of 80 ft/sec from an original
(initial) height of 96 feet above the ground
s = - 16t² + 80 t + 96

s is still the vertical position (height above
ground) of the tossed object in feet (ft)

t is time in seconds (sec) that the object
has been in motion

How high above the ground will the ball be

83. 2 seconds after being thrown?
84. 4 seconds after being thrown
85. 6 seconds after being thrown? Describe
what this means in practical terms.

§ 6.4 Obj # 2 The Power Rule
for Exponents-p334

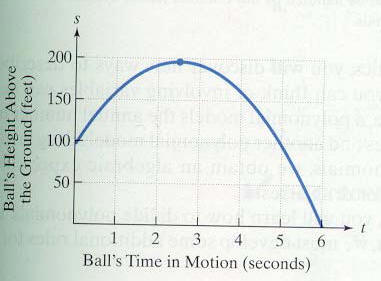
The graph visually displays
the information about the
thrown ball described in
Exercises 83-85. The
horizontal axis represents
the ball’s time in motion in
seconds. The vertical axis
represents the balls height
above the ground.

86. During which time
period is the ball rising?
87. During which time
period is the ball falling?
88. Identify your answer
from Exercise 84 as a
point oh the graph.
89. Identify your answer
from Exercise 83 as a
point oh the graph.
90. After how many seconds
doew the ball strike the
ground?
91. After how many seconds
does the ball reach its
maximum height above
the ground? What is a
reasonable estimate of
this maximum height?

On a sheet of paper for one Quiz point
Print your name and:

From TODAY’S lesson:
1) Describe one main math idea
2) Identify one math concept
or idea that interests you.
3) Ask at least one question
about the math we covered.