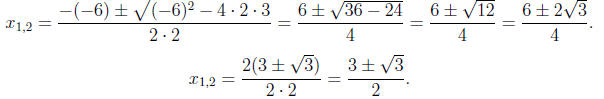Try the Free Math Solver or Scroll down to Resources!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Quadratic Equations

Definition. A quadratic equation in x is an equation that can be written in the form
ax² + bx + c = 0, where a ≠ 0.

Examples: x² + x = 2, x² + 6x + 5 = 0.
Zero Factor Theorem. If p and q are algebraic expressions, then

pq = 0 if and only if p = 0 or q = 0.

Example 3.1. Solving an equation by factoring.
Solve the equation x² + x = 2.

Note: To use the method of factoring, it is essential that only the number 0 appear on one
side of the equation.
x² + x = 2 subtract 2
x² + x - 2 = 0 factor
(x - 1)(x + 2) = 0 zero factor theorem
x - 1 = 0 or x + 2 = 0
x = 1 or x = -2
So the solutions to the given equation are 1 and -2.

Example 3.2. Solving an equation by completing the square.
Solve the equation x² + 6x + 5 = 0.

It is convenient to write the equation such that only terms involving x are on the right.
Thus we have

x² + 6x = -5.

We are trying to find a square of the type (x + a)² such that when expanded it contains
the terms x², 6x and a number. In this case, the square is (x + 3)², which expands as
x² + 6x + 9. So to complete the square we add 9 both sides and we obtain the following
equivalent equations:

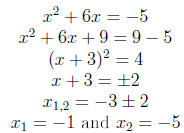
Quadratic Formula . If a ≠ 0, then the roots of ax² + bx + c = 0 are given by

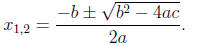
Note: If the discriminant b² - 4ac is negative, the equation does not have real roots, but
we will learn in the next section that if r is a positive number then we can use complex
numbers to define the principal square root of -r by 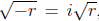, where i is a special
complex number with the property that i² = -1.

Example 3.3. Solving an equation using the quadratic formula.
Solve the equation 2x² - 6x + 3 = 0.
We have a = 2, b = -6, c = 3. Thus