Worksheet 4: Inverse Functions

Introduction: Background: (Refer to the text, Section 1.6)
In this worksheet we shall use Matlab to study functions y = f (x) and their inverses. Recall that a function is a
relation that associates each element in its domain with exactly one element in its range. Most relations in
mathematics are defined by equations. Some equations define functions; others do not.
For example, y = x^2 defines y as a function of x because x^2 produces a unique value.
However, the graph of the equation x^2 + y^2 = 1 is a circle of radius one with center at the origin.

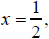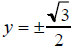Forthere are two y-valuesThus, a circle is not the graph of a function.

The x-values in the domain of a function y = f (x) are the input and the y -values in the range are the output
values. Therefore a function is a relation that associates each input with exactly one output. Thus, the graph of a
function must pass the so-called "vertical line test"; that is a vertical line can cross the graph of a function at
most once.

A function can also be thought of as a set of ordered pairs of numbers (x,y) where x is the input and y is the
corresponding output. When we graph a function we plot the values (x,y) (or some of them) and then connect
the points.

The concept of an "inverse function" may not be new to you because you already know the inverse relationship
between logs and exponentials,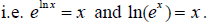

A function g(x) is the inverse of a function f (x) if
 i) f (g(x)) = x for all x in the domain of g, and
 ii) g( f (x)) = x for all x in the domain of f.

If a function y = f (x) has an inverse, the inverse is denoted by y = f^-1(x).

Thus, f ( f^-1(x)) = x for all x in the domain of f^-1 and f^-1( f (x)) = x for all x in the domain of f (x).

Another way of stating the inverse relationship is:

for x = a in the domain of f we have: b = f (a) if and only if a = f^-1(b).

So, if (a,b) is a point on the graph of f , then (b,a) is a point on the graph of f^-1 .

In terms of Matlab commands, if plot (x,y) produces the graph of f then plot (y,x) (with some care) produces
the graph of f^-1.

In Problem 1 you are asked to examine the relationship between the graphs of a function and its inverse.

Finally, by the "inverse correspondence" of a function f we mean the set of all points (y, x), where the point
(x,y) is on the graph of f. We say that a function f has an inverse provided the "inverse correspondence" is
also a function. In Problem 2, you are asked to identify which of several functions has an inverse function.

When does a function have an inverse? One-to-one functions

A function f is called a one-to-one function (written 1−1) provided it does not take on the same y-value twice;
that is f (x₁ ) ≠ f (x₂ ) whenever x₁ ≠ x₂.

Every function f has a unique output value, y = f (x) , for every input value x . A one-to-one function has the
added property that output values are never repeated

For example f (x) = x^2 is not 1−1 on the domain [−2,2]. For example, f (−1) = f (1) .

Only 1−1 functions have inverses.

Whether a function is or is not 1−1 may depend upon the domain selected for the function.

Instructions:

You may bring your completed worksheet to the Emporium when you take the quiz. Therefore it is
recommended that you:

• Number each problem clearly and circle answers.
• Use Matlab-generated graphs pasted into the document. Be sure to include the Matlab input commands that
you used to create the output. See worksheet 1 if you need help "copying" graphs.
• Answer all questions completely.

Example: In this example we will use Matlab to graph a function f and its inverse correspondence and then
answer the following questions for the function f (x) = x^3 +1 on the domain 0 ≤ x ≤ 2 :

a) Is the inverse correspondence a function?
b) What is the range of f ?
c) What is the domain of f^-1? What is the range of f^-1?

Solution:
a) To discover if the inverse correspondence is a function, we shall graph f and check to see if it is 1−1.

>> x=0:.01:2; >> y=x.^3+1; >> plot(x,y),axis([-1,3,0,10])

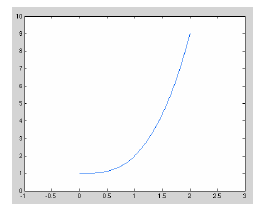This graph is clearly the graph of a1−1 function because it is an increasing graph with no repeated y values.
When a graph is either always increasing or always decreasing, we say it is monotonic.

b) From the graph we see that the range of f is 1 ≤ y ≤ 9.

c) Since f is 1−1 then the inverse correspondence is also a function. (x,y) is on the graph of f if and only if
(y,x) is on the graph of f^-1, we can therefore get the graph of f^-1 by using plot(y,x).

We also want the line y = x on the graph. We get this by using the command plot(z,z) where z = 0:9 to fill the
Matlab screen. We can combine these commands into one command.

>> x=0:.01:2; >> y=x.^3+1; >> z=0:9; >> plot(x,y,y,x,z,z) >> hold on >> title('blue:f(x), green:f^-1(x), red:y=x') >> text(1.75,5,'f(x)'),text(4,1.75,'f^- 1(x)'),text(5.8,5.8,'y=x') >> hold off

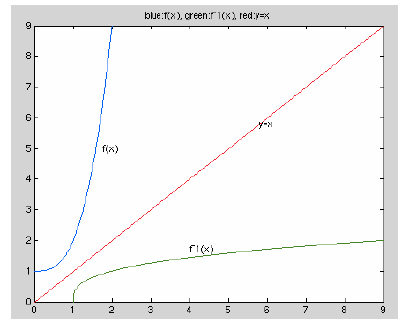From the graph of f^-1, we see that the domain of f^-1 is 1 ≤ x ≤ 9 and the range is 0 ≤ y ≤ 2.

Problems:
Problem 1:

(a) In each (i) - (iii) you are given a function y = f (x) and a domain for f .
In each case, graph f , f^-1 , and the line y = x by defining the given x and z arrays, then the function y, followed
by the command:

»plot(x,y,y,x,z,z)
It may be helpful to add x and y-axes to your graph.

By hand on your printout, label the graph of y = f (x) and the graph of y = f^-1(x).
From your graph, answer each of the following questions:
What is the range of f ? What is the domain of f^-1 ? What is the range of f^-1?

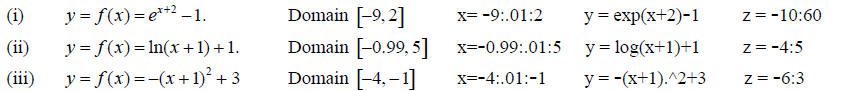
(b) Based on your graphs, what symmetry is there between the graph of a function and its inverse in the xy-plane?
(c) What is the relationship between the domain and range of a function and the domain and range of its
inverse?

Problem 2:

Let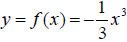with domain [−3, 3].

(a) Use Matlab to graph y = f(x) on its domain. (Do not paste this graph into your worksheet yet.)
From your graph, what is the range of f?
Using your answer from (c) in problem 1, give the domain and range of y = f^-1(x).

(b) Recall that for a value x in the domain of f, y = f(x) if and only if x = f^-1(y). Or, for two numbers a and b,
b = f (a) if and only of a = f^-1(b). Since you do not have a formula for f^-1, you cannot find f^-1(b) directly.
However, you can determine the value of f^-1(b) by solving f (x) = b for x .
For the given function f, use the fzero command and format short command to find f^-1(b) for each of the
values b = −6, − 4, 0, 3, 5. Your final answer should be in the form of a table having its first column the
values for b and second column the values of f^-1(b) to 4 decimal place accuracy.

Recall the fzero command has the form fzero( 'function' , x0) and identifies points where the function crosses
the x-axis. It requires the variable to be x and the function to equal zero. x0 is a guess and should be close to
the answer. So the set-up should be as follows:

>> format short
>> fzero('(-1/3)*x.^3-(-6)',[-3,3])
ans = 2.6207

Now change the -6.

(c) Apply the command axis([-9,9,-9,9]) to the graph of y = f(x) obtained in (a);
paste the resulting graph into your worksheet; and on the same graph sketch, by hand, a graph of y = f^-1(x) by
plotting the points obtained in (b).

Problem 3:

(a) In each of (i)-(iv) you are given a function f and an x array. Graph both f and its inverse correspondence
using the command:

»plot(x,y,y,x)
In each case state whether the inverse correspondence is a function by applying the vertical line test to the graph
of the inverse correspondence.

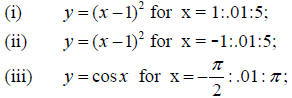(Recall π is pi in Matlab.)

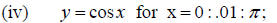
(b) In your own words describe a test (similar to the vertical line test) that can be applied to the graph of the
original function, y = f (x) , to determine whether the inverse correspondence of f will be a function.