Linear Algebra

• Elements
>Scalars, vectors, matrices
• Operations
>Addition & subtraction (vector, matrix)
>Multiplication (scalar, vector, matrix)
>Division (scalar, matrix)
• Applications
>Signal processing, others...

Scalars & Vectors
•  Scalar: fancy word for a number:
>e.g., 3.14159, or -42.
>Scalar can be integer, real, or complex.
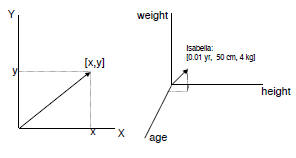
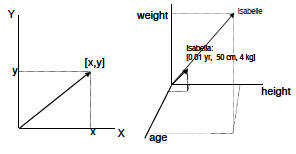
•  Vector: a collection of numbers:
>[age, height, weight] or [x, y, z, roll,
pitch, yaw]
>Why bother?

• Compact notation: p = [x, y, z, roll, pitch, yaw]
> So p_i is the ith element, e.g., in above, p₂=y
• Ease of manipulation (examples later).

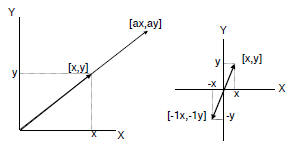
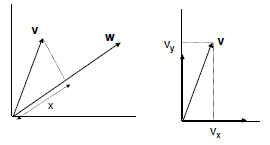
Visualize a vector

Vectors
• Row vector: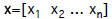
• Column vector: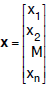
• The transpose operator:
>If 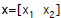, then

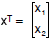
Operations: Scalar multiplication
• Vector multiplied by scalar:
>Multiply each vector element by the
scalar:
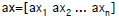
• Scalar multiplication increases length
of vector.
• If the scalar is negative, also
reverses direction of the vector.

Scalar multiplication
-

Addition of vectors
• Element-by-element:
>So,
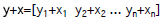
>Associative, commutative
>Add two like-shape vectors (row & row).

Linear combinations
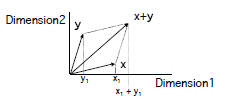
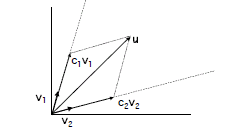
• Linear combinations of vectors:
>Example: u = c₁v₁ + c₂v₂

Linear independence
• Set of all linear combinations of a
set of vectors is the linear space
spanned by the set.
• A set of vectors is linearly
independent if none of the vectors
in the set can be written as a linear
combination of the other members
of the set.

Inner product
•Also called “dot product:”
> x•y = x₁y₁ + x₂y₂ + … + x_ny_n
• Maps two vectors to a scalar.
• Length (also called norm):
> x•x = x₁x₁ + x₂x₂ + … + x_nx_n
>x•x = ||x||²
> ||x|| is the length of the vector
> Note ||ax||=|a| ||x||

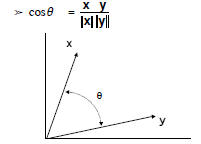
Angle between two vectors
• Defined using inner product:

Example of compact notation
• Set of data: x=[x₁,…,x_n], y=[y₁,…,y_n]
• Correlation coefficient:

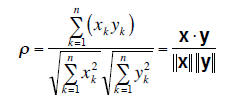
Basis vectors
• A basis for V is a set of vectors B in V that
span V. Vectors in B are linearly
independent, so any v in V can be written as
a linear combination of vectors in B.
• Orthogonal bases -> simple combinations.
> Orthogonal if u•v = 0, as cos θ = 0.
• Usual basis (of infinitely many) for R3 is:
>B = [1,0,0]^T , [0,1,0]^T , [0,0,1]^T
> coefficients of v using B are coordinates.

Projections of vectors
• Projection of v onto w:
>In 2 dimensions, x = ||v|| cos θ, or in higher
dimensions is:

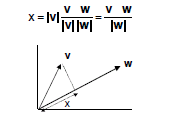
Projection onto basis

Matrices
• Matrices are arrays of numbers.
>Convenient, compact notation.

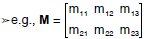
• Are operators, mapping between vector
spaces (e.g., change of basis or
coordinates).
• Some special names:
>Square has same number of rows and
columns.
>Diagonal has non-zero elements only on
diagonal.
• if elements are all = 1, call it I identity matrix,
mapping vector space to itself.
>Symmetric is square with

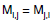
Matrix operations
• If one considers a matrix as a set of
vectors:
>Can multiply matrix by scalar.
>Can add conforming matrices (same #
rows, columns).
• Multiply vector by matrix:

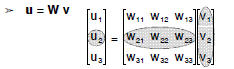
Matrix multiplication
• Can concatenate mappings:
> If we have, u = Wv and v = Mz, then
u = W(Mz) = Pz
• W must have same number of rows as
M has columns, so multiplying an rxs
matrix by sxt matrix gives an rxt matrix.
>Associative, distributive, but not
commutative!

Inner and outer product
• Inner product: Maps two vectors to a
scalar:

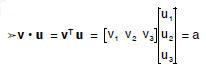
• Outer product: Maps two vectors to a
matrix:

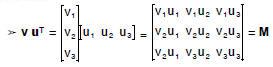
Matrix inverse
• The inverse of M is that matrix which,
when multiplied by M, gives the identity
matrix:
> MM^-1 = M^-1 M = I
• Use the inverse for the solution to n
simultaneous linear equations:
>If y = A x, then x = A^-1 y.
• M^-1 may not exist, then M is singular.

Eigenvectors & eigenvalues
•Matrix mapping u = Wv takes domain V to
range U.
• Generally, elements in V are changed in
length and direction.
• Elements that are changed in length only are
called eigenvectors of W.
>If 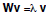, then v is an eigenvector of W with
eigenvalue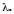
• W can have more than one eigenvector; they
form a basis for the column space of W.