Quadratic Functions
4 Graph
Some quadratic functions are shown in figure 1:
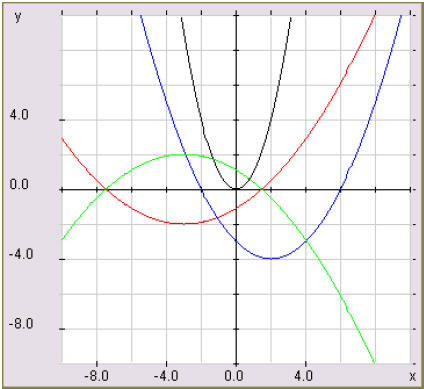
Figure 1: Some Quadratic Functions
Looking at the various graphs we have, we can draw several conclusions.
• There seems to be two kind of graphs. Some open up, the
others open
down.
• All the graphs seem to have a similar shape, that of a U. Besides the way
they open, another important factor in characterizing these graphs seems
to be the position of the graphs with respect to both axes. Some graphs
intersect the x-axis twice, others once, some never. All graphs intersect
the y-axis once.
It turns out that it is fairly easy to predict how the graph will look if we
have its equation. This is what we study next.
4.1 Orientation
• If a > 0 the parabola opens up.
• If a < 0 the parabola opens down.
Example 15 The graph of y = x2 − 4 opens up.
Example 16 The graph of y + 2x2 − 5x = 3 opens down.
4.2 The y-intercept
Remember, to find the y-intercept, we set x = 0 and solve for y. If we do this
in y = ax2 +bx+c, we have that y = c. So, the y-intercept of y = ax2 +bx+c
is the point (0, c). This tells us that when the equation is in standard form,
we
get the y-intercept with no computations.
Example 17 The y-intercept of y = x2 − 4 is (0,−4)
Example 18 The y intercept of y +2x2 − 5x = 3 is (0, 3)
4.3 X-intercepts
Remember, to find the x-intercepts, we set y = 0 and solve for x. To find the
x-intercepts of y = ax2 + bx + c, we need to solve ax2 + bx + c = 0. This is a
quadratic equation, its solutions are given by the quadratic formula.
Example 19 Find the x-intercepts of y = x2 − x − 6.
To find them, we need to solve x2 − x −6 = 0. We already solved this equation
above, and found that its solutions were x = −2 and x = 3. Therefore, the
x-intercepts are (−2, 0) and (3, 0).
Example 20 Find the x-intercepts of y = x2 + x+ 1.
To find them, we need to solve x2 + x +1 = 0. We already solved this equation
above, and found that it had no solutions. Therefore, y = x2 + x + 1 has no
xintercepts.
We can even tell more about it. Since the coefficient of x2 is positive,
it means that its graph opens up. Hence, the graph is entirely above the x-axis.
4.4 Vertex
Definition 21 (vertex) The vertex is the highest point on a parabola if the
parabola opens down, it is the lowest point if the parabola opens up. See Figure
2. The vertex is a point, hence finding the vertex means finding its x and y-
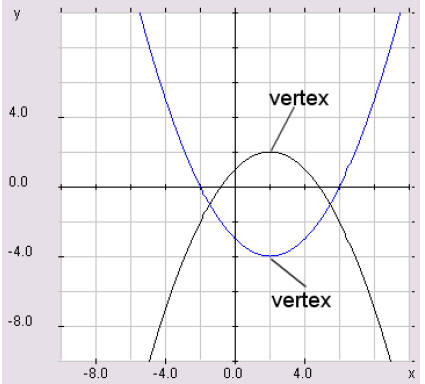
Figure 2: Vertex of Quadratic Functions
coordinates.
• The x-coordinate of the vertex is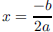 
.
• To find the y-coordinate of the vertex, simply plug the x-coordinate in
the equation and compute y. If the quadratic function is y = f (x) =
ax2 + bx + c, then the coordinates of the vertex are
.
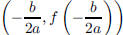• If the quadratic function is in vertex form, then the coordinates of the
vertex are (h, k).
Example 22 Find the vertex of y = x2 + x + 1.
Here, a = b = c = 1. Hence, the x-coordinate of the vertex
is
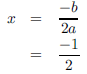
The y-coordinate of the vertex is then
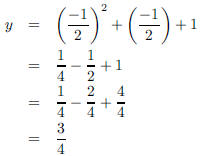
The coordinates of the vertex are:
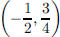. In this case, knowing the vertex
also provides information about the x-intercepts. Since this parabola opens up,
and its vertex (lowest point) is above the x-axis, the entire parabola has to be
above the x-axis. Hence, it cannot have x-intercepts.
Example 23 Find the vertex of y = x2 − 8x+ 16.
Here, a = 1, b = −8, c = 16. The x-coordinate of the vertex is
.
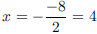The y-coordinate of the vertex is y = 42 − (8) (4) + 16 = 0. So, the vertex is
(4, 0). Note that since the y-coordinate of the vertex is 0, the vertex is on
the
x-axis, hence it is also an x-intercept.
Example 24 Find the vertex of y = 2(x − 3)2 + 5
This function is in vertex form, with h = 3 and k = 5. The vertex is (3, 5).
Remark 25 If a parabola opens up (a > 0) and its vertex is above the x-axis
(its y-coordinate > 0) then the parabola has no x-intercepts.
Remark 26 If a parabola opens down (a < 0) and its vertex is below the x-axis
(its y-coordinate < 0) then the parabola has no x-intercepts.
Remark 27 We can combine the previous two remarks into one which states:
If a and the y-coordinate of the vertex have the same sign, the corresponding
parabola has no x-intercepts.
Remark 28 Finally, if the vertex is on the x-axis (its y-coordinate is 0) then
there is only one x-intercept, the same as the vertex.
The above remarks tell us that we should always find the vertex before the
x-intercepts. In some cases, knowing the vertex allows us to draw conclusions
about the x-intercept.
4.5 Technology Note
I have developed several applets to experiment with quadratic functions:
1. To experiment with the role a, b, and c play in the graph of y = ax2+bx+c.
2. To experiment with the role a, h and k play in the
graph of y = a (x − h)2+
k.
3. To experiment with a graphing applet which can graph
any function, similar
to the TI 83.
5 Maximum, Minimum and Range
Consider the quadratic function y = f (x) = ax2 + bx + c. Remember that the
y-coordinate of a point gives us the vertical position of that point. When a
parabola opens up, its vertex is the lowest point, hence its y-coordinate
corresponds
to the smallest value y (i.e. the quadratic function) can have. Similarly,
if the parabola opens down, the y-coordinate of its vertex corresponds to the
largest value y (i.e. the quadratic function) can have. We summarize this by:
• If a > 0, the quadratic function f (x) = ax2 + bx + c has no maximum.
Its minimum is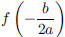 
(the y-coordinate of the vertex) . Its range is
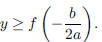
• If a < 0, the quadratic function f (x) = ax2 + bx + c has no minimum.
Its maximum is 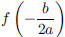(the y-coordinate of the vertex) . Its range is
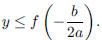
So, questions related to finding the maximum or minimum of a quadratic
function are solved by finding the vertex of the function.
Example 29 Find the maximum, the minimum and the range of f (x) = −x2+
4x + 2.
Here, a = −1, b = 4, c = 2. The x-coordinate of the vertex is
.
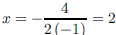The y-coordinate is −22 +4(2)+2 = 6. Hence the vertex is (2, 6). Since the its
graph opens down, f (x) has no minimum. Its maximum is f (x) = 6. Its range
is all reals less than or equal to 6.